(-4.5; 7.25)
Пошаговое объяснение:
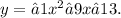
Координаты вершины параболы - это ее экстремум, точка в которой производная функции обращается в ноль.
То есть это точка с координатами

где х0 - решение уравнения
у'(х) = 0.
1) Найдем производную: '
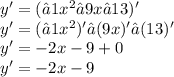
2) Найдем корни уравнения у'(х)=0
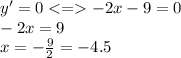
3) Найдем значение у в точке х = -4.5:
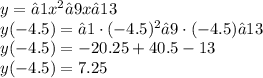
То есть искомая точка имеет координаты
(-4.5; 7.25)
Дополнительно можно проверить ответ на корректность. Для этого вычислим значения у для х правее и левее х0
Например, для х=-5 и х=-4
Получим, что
у(-5) = 7 < у(-4.5)
у(-4) = 7 < у(-4.5)
И справа и слева у меньше чем в точке х=4.5.
Значит мы верно нашли вершину параболых
а) ответом на этот пример будет отношение коэффициентов при старших степенях переменной числителя и знаменателя, поскольку в числителе и знаменателе - стандартные многочлены 4-й степени и х стремится к ∞; 8/2=4
б)Разложим предварительно многочлены на линейные множители.
3х²+5х-42=0; х₁,₂=(-5±√(25+3*4*42) )/6=(-5±√529)/6=(-5±23)/6; х₁=3; х₂=-14/3; 3х²+5х-42=3*(х-3)(х+14/3)=(х-3)(3х+14); х²-5х+6=0, по теореме, обратной теореме Виета х₁=2; х₂=3; х²-5х+6=(х-2)(х-3). Разделим числитель на знаменатель, с учетом разложений.
(3х²+5х-42)/(х²-5х+6)=(х-3)(3х+14)/(х-2)(х-3)=(3х+14)(х-2). предел от (3х+14)(х-2) при х стремящемся к 3, равен (3*3+14)(3-2)=9+14=23
в) разложение числителя х²-3х+2 , предварительно с подсчитанными по теореме, обратной теореме Виета корнями уравнения х²-3х+2=0, х₁=1; х₂=2, примет вид х²-3х+2=(х-1)*(х-2). Домножим числитель и знаменатель на скобку (√(5-х)+√(х+1)), сопряженную знаменателю. В знаменателе вырисовалась разность квадратов (а-в)*(а+в)=а²-в², т.е. (5-х)-(х+1)=5-х-х-1=4-2х=-2*(х-2), а числитель примет вид
(√(5-х)+√(х+1))*(х-1)(х-2). После деления числителя на знаменатель получим
((√(5-х)+√(х+1))*(х-1)(х-2))/(-2*(х-2))=-((√(5-х)+√(х+1))*(х-1))/(2*(х-1)), подставим вместо х=2, получим -(√3+√3)(2-1)/(2*(2-1))=-2√3/2=-√3
2) 8 * 2 = 16 см - периметр
ответ: 16 см периметр прямоугольника