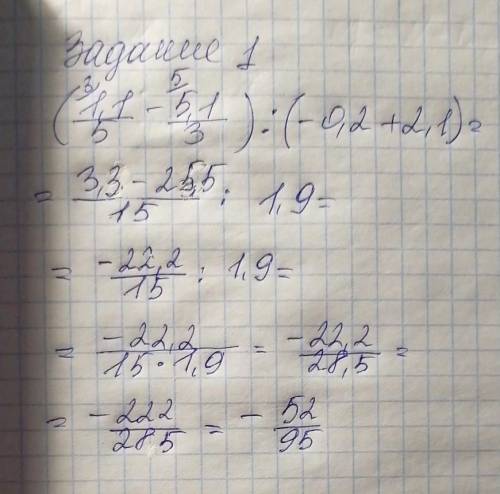ответ. \{6\}.
Пошаговое объяснение:
Решение. Сначала найдем корни уравнения x^2-2x-4=0. Это 1\pm\sqrt{5}. Следовательно, условие x^2-2x-4\ge0 выполняется при x\le1-\sqrt{5} и при x\ge1+\sqrt{5}, а условие x^2-2x-4<0 — при 1-\sqrt{5}<1+\sqrt{5}. Рассмотрим два случая:
1) x\in\left(-\infty;1-\sqrt{5}\right]\cup\left[1+\sqrt{5};+\infty\right).
Исходное уравнение на этом множестве имеет вид x^2-2x-4=3x-2.
Его корни \displaystyle x_{1,2}=\frac{5\pm\sqrt{33}}{2}. Из них только \displaystyle\frac{5+\sqrt{33}}{2} попадает под наш случай. Докажем это:
\[\begin{array}{c} \displaystyle 1-\sqrt{5}<\frac{5-\sqrt{33}}{2}<1+\sqrt{5}\Leftrightarrow\\[2mm] \Leftrightarrow2-2\sqrt{5}<5-\sqrt{33}<2+2\sqrt{5}\Leftrightarrow\\ \Leftrightarrow-3-2\sqrt{5}<-\sqrt{33}<-3+2\sqrt{5}\Leftrightarrow\\ \Leftrightarrow3+2\sqrt{5}>\sqrt{33}>3-2\sqrt{5}. \end{array}\]
Так как \sqrt{5}>2, то 3-2\sqrt{5}<0, и, действительно, \sqrt{33}>0>3-2\sqrt{5}. Для доказательства левой части двойного неравенства возведем его в квадрат (это можно сделать, поскольку обе части неравенства неотрицательны):
Задание 1.
во вложениях
Задание 2.
Пусть 3х - яблонь в саду, тогда х - груш.
По условию задачи, когда вырубили 14 яблонь и посадили 10 груш, деревьев стало поровну.
Составим и решим уравнение:
3х - 14 = х + 10
3х - х = 10 + 14
2х = 24
х = 12 - количество груш в саду
Т. к. по условию задачи яблонь в 3 раза больше, чем груш, то:
12 × 3 = 36 - количество яблонь в саду
ответ: 12 груш и 36 яблонь.
Задание 3.
а) 3( х + 0,6) = 3 - х
3х + 1,8 = 3 - х
3х + х = 3 - 1,8
4х = 1,2
х = 0,3
ответ: 0,3.
б) во вложениях
Задание 4.
2,5 : 8,75 = х : 21
х = 2,5 × 21 ÷ 8,75
х = 6
ответ: 6.