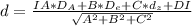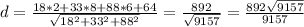Відповідь:
1 та 2
Пояснення:
Розкладемо ліву частину нерівності на множники, розв'язавши відповідне квадратне рівняння:
-2x²+5x-2 = 0
2x²-5x+2 = 0
D = b²-4ac = (-5)²-4·2·2 = 25-16 = 9
x_1 = (-b+√D)/2a = (5+√9)/(2·2) = (5+3)/4 = 2
x_2 = (-b-√D)/2a = (5-√9)/(2·2) = (5-3)/4 = 0,5
Тоді -(2x²-5x+2) = -2(x-0,5)(x-2) = (2x-1)(2-x)
Тепер нерівність перетворена до такої: (2x-1)(2-x) ≥ 0
Розв'яжемо її методом інтервалів. Позначимо нулі функції в лівій частині нерівності (корені щойно розв'язаного рівняння) на числовій прямій та з'ясуємо знак цієї функції на кожному з проміжків, які утворяться (проставимо "+" або "-").
- + -
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯(0,5)¯¯¯¯¯¯¯¯¯¯¯¯¯¯(2)¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Множиною розв'язків буде проміжок, на якому функція набуває невід'ємних значень. Тобто x ∈ [0,5; 2]. Йому належать лише два цілих числа: 1 та 2.
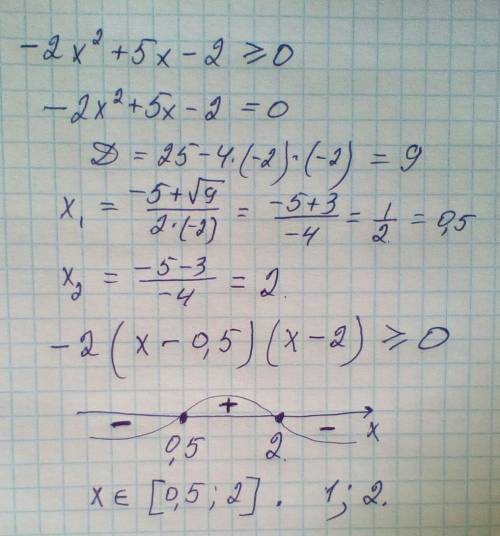
Пошаговое объяснение:
1)уравнение плоскости Q, проходящей через точки
А (–6; –4; 2);
В (5; –2; –1);
С (5; 6; –4);
для составления уравнения плоскости используем формулу
![\left[\begin{array}{ccc}x-z_A&y-y_A&z-z_A\\x_B-x_A&y_B-y_A&z_B-z_A\\x_C-x_A&y_C-y_A&z_C-z_A\end{array}\right] =0](/tpl/images/1627/6356/c8719.png)
![\left[\begin{array}{ccc}x-(-6)&y-(-4)&z-2\\5-(-5)&(-2)-(-4)&-1-2\\5-(-6)&6-(-4)&-4-2\end{array}\right] =0](/tpl/images/1627/6356/67f4b.png)
(x -(-6))(2*(-6) - (-3)*10) - (y -(-4))(11*(-6) -(-3)*11 ) + (z -2)(11*10 -2*11) = 0
18(x -(-6)) + 33(y - (-4)) + 88(z - 2) = 0
и вот мы получаем уравнение плоскости Q
Q : 18x + 33y + 88z +64 = 0
2) канонические уравнения прямой АВ. А(–6; –4; 2); В(5; –2; –1);
формула канонического уравнения прямой

наша формула прямой
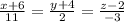
3) уравнение плоскости G, проходящей через точку D(2; 8; 6) перпендикулярно прямой АВ
будем искать прямую в виде 
здесь А, В, С - координаты направляющего вектора.
поскольку G ⊥ АВ, то нормаль АВ будет направляющим вектором для G ⇒ s = n = (11, 2, -3)
и вот формула
G : 11y + 2y - 3z -20 =0
4) расстояние от точки D(2; 8; 6) до плоскости Q : 18x + 33y + 88z +64=0
для расчета нам потребуется
А = 18; В = 33; С = 88; D = 64;