Найдем площади фигур суммируя площади фигур В них.
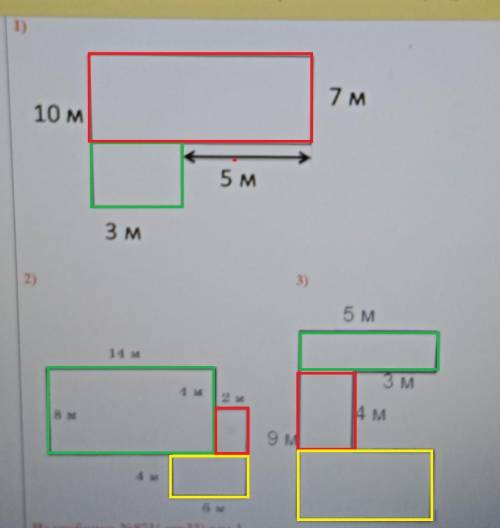
1) Найдем для начала маленькую площадь первой фигуры. (зеленый цвет на моем скрине)
Мы знаем ее длину 3 м, найдем ее ширину. 10 м - 7 м = 3 м.
Находим ее площадь 3*3=9 м2
Теперь находим площадь большого прямоугольника. (красный цвет)
Мы знаем его ширину 7см. Найдем его длину 5+3= 8м.
Находим площадь 7*8=56 м2. Складываем площади двух фигур: 9+56=65 м2
2) Теперь вторая фигура, находим площадь прямоугольника (зеленый),
8 м * 14 м = 112 м2
Теперь найдем площадь красной фигуры.
Мы знаем ее длину = 2 м. Ширину же находим: 8 - 4 = 4 м
Площадь равна 2м*4м=8м2
И находим площадь желтой фигуры.
4м*6м=24м2.
Суммируем площади: 112м2+8м2+24м2=144м2
3) Найдем площадь красной фигуры. Ее ширина равна 4 м.
Длина же будет равна 5м-3м=2м. Площадь: 4м*2м=8м2
К СОЖАЛЕНИЮ, я дальше не могу точно сказать ширину остальных фигур, только логически догадаться.
Пусть у желтой фигуры 3 м = ширина. Длина у нее 5 м. Площадь: 3м*5м=15м2
Зеленая фигура имеет длину 5м. Ширина же будет равна 9-4-3=2м. Площадь равна 5м*2м=10м2.
Суммируем: 8м2+15м2+10м2=33м2.
, сверься у учителя насчет последней фигуры, в ней я не до конца уверен
Пошаговое объяснение:
Буратино может разделить свои монеты на три кучки по 7, 4, 4, или по 5, 5, 5, или по 3, 6, 6, или по 1, 7, 7 монет. При первом взвешивании он положит на весы две кучки монет одинаковой величины. Если при этом весы оказались в равновесии, значит, все монеты на весах настоящие, а бракованная монета в оставшейся кучке. Тогда при втором взвешивании на одну чашку весов Буратино положит кучку с бракованной монетой, а на вторую — столько настоящих монет, сколько всего монет он положил на первую чашку, и тогда он сразу определит, легче фальшивая монета, чем настоящие, или тяжелее. Если же при первом взвешивании весы оказались не в равновесии, значит, все монеты в оставшейся кучке настоящие. Тогда Буратино уберёт с весов лёгкую кучку, а монеты из тяжёлой кучки разделит на две равные части и положит на весы (если в кучке было 5 или 7 монет, предварительно добавит к ним одну настоящую монету). Если при втором взвешивании весы оказались в равновесии, значит, фальшивая монета легче настоящих, а если нет, то тяжелее.
1 4/5 - 2 3/4 = 9/5 -11/4 = 36/20 - 55/20 = -19/20
2 2/19 * ( -19/20) = 40/19 * 19/20 = - 2
1 8/11 + ( - 2 ) = 19/11 -2 = 19/11 -22/11 = -3/11