12 см
Пошаговое объяснение:
По закону Паскаля сила давления жидкости зависит только от глубины и площади поверхности.
То есть, в данной точке аквариума вода одинаково давит на дно и на любую боковую стенку.
Поэтому фраза "чтобы сила давления воды на дно была меньше силы давления на все стенки в 2 раза" означает "чтобы площадь дна была в 2 раза меньше, чем площадь всех боковых стенок".
Длина аквариума 30 см, ширина 20 см, площадь 30*20=600 кв.см.
Высота воды h см, площадь боковых стенок равна
30h + 20h + 30h + 20h = 100h кв.см.
И по условию, эта площадь должна быть в 2 раза больше дна.
100h = 2*600 = 1200
h = 12 см
20
Пошаговое объяснение:
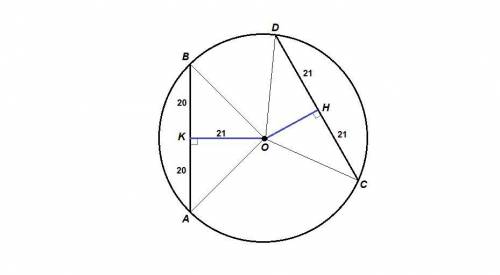
Соединим центр окружности с концами хорд.
ОА = ОВ = ОС = OD как радиусы.
Проведем ОК⊥АВ и и OH⊥CD,
ОК = 21 - расстояние от центра до АВ,
ОН - искомое расстояние от центра до CD.
ΔОАВ равнобедренный, значит ОК - высота и медиана. ⇒
АК = КВ = 1/2АВ = 1/2 · 40 = 20
Из прямоугольного треугольника АКО по теореме Пифагора:
АО = √(АК² + КО²) = √(20² + 21²) = √(400 + 441) = √841 = 29
СО = АО = 29
ΔCOD равнобедренный, значит OН - высота и медиана, ⇒
СН = HD = 1/2CD = 1/2 · 42 = 21
Из прямоугольного треугольника СОН по теореме Пифагора:
OH = √(CO² - CH²) = √(29² - 21²) = √(841 - 441) = √400 = 20
Правильная призма - это призма, в основании которой лежит правильный многоугольник (в нашем случае - квадрат), а боковые ребра перпендикулярны основанию. То есть это прямая призма, в основании которой лежит квадрат.
Скрещивающиеся прямые - прямые, которые не лежат в одной плоскости и не имеют общих точек или другими словами это две прямые в пространстве, не имеющие общих точек, и не являющееся параллельными. В нашем случае АВ (сторона основания) и DВ1 (диагональ призмы) - скрещивающиеся прямые. Расстоянием между скрещивающимися прямыми называется расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой. В нашем случае плоскость, проходящая через В1D параллельно АВ - это плоскость DА1В1С.
Расстояние от точки до плоскости, не содержащей эту точку, есть длина отрезка перпендикуляра, опущенного из этой точки на данную плоскость. В нашем случае искомое расстояние - это перпендикуляр АН из точки А к диагонали А1D боковой грани АА1D1D).
Решение:
Площадь квадрата равна 90, значит его сторона (сторона основания) равна √90=3√10.
По Пифагору А1D=√(АА1²+АD²)=√(10+90)=10.
АН - высота вз прямого угла в треугольнике АА1D и по свойству этой высоты равна
АН=АА1*АD/А1D или АН=3√10*√10/10=30/10=3.
ответ: Искомое расстояние равно З.
Второй вариант - координатный метод.
Привяжем нашу призму к системе координат.
Тогда имеем точку А(0;0;3√10) и плоскость, проходящую через точки
B1(0;√10;0), C(3√10;0;0) и D(3√10;0;3√10).
Надо найти расстояние от точки А до этой плоскости.
Уравнение плоскости по формуле:
|X-X1 X2-X1 X3-X1|
|Y-Y1 Y2-Y1 Y3-Y1| =0.
|Z-Z1 Z2-Z1 Z3-Z1|
В нашем случае:
|X-0 3√10-0 3√10-0|
|Y-√10 0-√10 0-√10 | =0.
|Z-0 0-0 3√10-0|
Раскрываем определитель по первому столбцу:
(X-0)*| -√10 -√10| - (Y-√10)*|3√10 3√10| + (Z-0)*|3√10 3√10| =0.
| 0 3√10| | 0 3√10| |-√10 -√10|
Далее:
(X-0)*(-30) - (Y-√10)*(90) + (Z-0)*(-30-(-30) = 0. Или
-30X - 90Y+90√10 + Z*0 = 0.
То есть имеем уравнение плоскости вида:
Аx+By+Cz+D=0, где А=-30, В=-90, С=0 и D=90√10.
Расстояние от точки А((0;0;3√10) до плоскости определяется по формуле:
d = |A*Xa+B*Ya+C*Za+D|/√(A²+B²+C²) или
d = |-30*0+(-90)*0+0*3√10+90√10|/√(900+8100+0) или
d= (90√10)/(30√10) = 3.
ответ: искомое расстояние равно 3.