Предположим, что у нас есть функция (график этой функции – это парабола) и необходимо построить график функции . Вычислим значения некоторых точек для графиков этих функций.
Из таблиц видно, что одним и тем же значениям аргумента соответствуют противоположные значения функций. Графически это означает, что графики расположены симметрично относительно оси абсцисс. То есть заданная парабола () зеркально отобразится относительно оси (см. Рис. 1).
Рис. 1. Графики функций и
Таким образом, если у нас есть произвольный график , то для построения графика необходимо график симметрично отразить относительно оси (см. Рис. 2). Такое преобразование называется преобразованием симметрии относительно оси .
Рис. 2. Преобразование симметрии относительно оси
Преобразование симметрии – зеркальное отражение относительно прямой. График получается из графика функции преобразованием симметрии относительно оси .
На рисунке 3 показаны примеры симметрии относительно оси .
Рис. 3. Симметрия относительно оси Ox
ответ: 450; 300; 225; 180; 113.
Пошаговое объяснение:
От 100 до 999 имеются 900 чисел. (Используем "правило плюс один". Это правило используется для подсчета количества чисел в числовом ряду с учетом шага. Шаг это закономерность числового ряда. К примеру, если взять ряд чисел 1 2 3 4 5 6 7 8 9 10, то шагом является +1. Для подсчета используем простую формулу: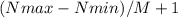 
. Где M - это шаг. 
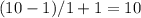, значит 10 чисел.
Теперь перейдем к пунктам.
1) При делении на 2, остаток 1.
Заметим, что от 100 до 999 число начинается с четного, а заканчивается нечетным. Это делает пример очень удобным для подсчета. Отсюда следует, что половина всех чисел это нечетные (то есть с остатком 1) ответ: 450 чисел.
2) При делении на 3, остаток 2.
Разобьем 900 чисел на группы по 3 числа
100 101 102
103 104 105
106 107 108
и так далее. Первое число при делении на 3 дает остаток 1, второе число остаток 2, а третье число нацело делится и так далее. Последнее число 999 делится нацело на 3, таким образом, заключительная группа из трёх чисел будет таким:
997 998 999. При делении 997 на 3 - остаток 1, 998 на 3 - остаток 2. Это значит, что каждое второе число в группе дает остаток 2. 900/3 = 300.
ответ: 300 чисел.
3) При делении на 4, остаток 3.
Таким же образом делим на группы по 4 числа.
100 101 102 103
104 105 106 107
108 109 110 111
и так далее.
996 997 998 999. 1-ое число делится нацело, 2-ое число - остаток 1, 3-е число - остаток 2, 4-ое число - остаток 3. 900/4 = 225.
ответ: 225 чисел.
4) При делении на 5, остаток 4.
100 101 102 103 104
105 106 107 108 109
...
995 996 997 998 999.
900/5 = 180.
ответ: 180 чисел.
5) При делении на 8, остаток 7.
Тут чуток иначе, но принцип тот же. Если посчитаем, то первое число 100 при делении на 8 выдает остаток 4. Значит у каждого последующего числа остаток будет на 1 больше, максимальный остаток - 7. Число 104 уже разделится нацело. Чтобы использовать удобный подсчет с использованием "правило +1", начнём с минимального числа, делящегося на 8 - это 104, заканчивая максимальным делящимся 8 - это 992. Подставляем в формулу: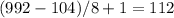 
. Теперь добавляем числа, которые не были взяты для подсчета с остатком 7, это 103 и 999. Теперь важный момент. При расчете количества чисел, мы начинали с числа, который делится нацело и заканчивали числом, тоже делящееся на 8. В последней группе чисел, начиная с 992 заканчивая 999, должно быть одно число, которое выдает остаток 7 - это 999. Значит 112 чисел от 104 до 999 и число 103. Всего 113 чисел.
ответ: 113 чисел.
2)12:4\11=12*11\4(сокращаем 12 и 4 будет 3)=3*11=33(уч.)-всего учеников в классе
ответ: 33 ученика. (может быть так)