1) 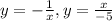
Определим точки пересечения функций. Для этого приравниваем оба функции и решаем полученное уравнение:
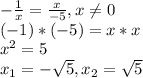
Тогда
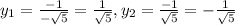
Нашли точки пересечения функций
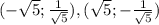
Чтобы начертить график функций определим некоторые значения:
| x | -2 | -1 | 1 | 2 |
| y=-1/x | 1/2 | 1 | -1 | -1/2 |
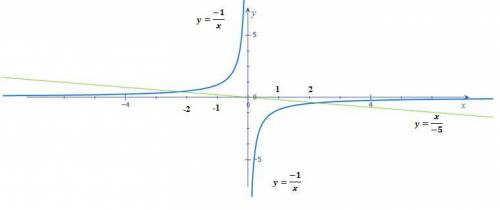
| y=x/(-5) | 2/5 | 1/5 | -1/5 | -2/5 |
График функций в приложенном рисунке 3.
2) 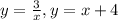
Определим точки пересечения функций. Для этого приравниваем оба функции и решаем полученное уравнение:
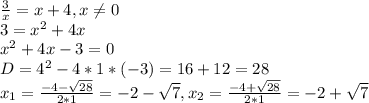
Тогда
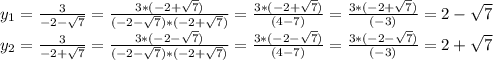
Нашли точки пересечения функций
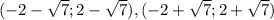
Чтобы начертить график функций определим некоторые значения:
| x | -2 | -1 | 1 | 2 |
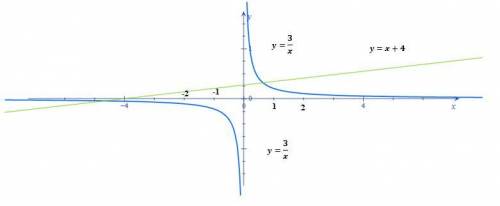
| y=3/x | -3/2 | -3 | 3 | 3/2 |
| y=x+4 | 2 | 3 | 5 | 6 |
График функций в приложенном рисунке 1.
3) 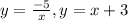
Определим точки пересечения функций. Для этого приравниваем оба функции и решаем полученное уравнение:
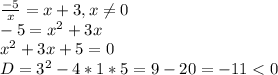
Отсюда следует, что функции НЕ ПЕРЕСЕКАЮТСЯ!
Чтобы начертить график функций определим некоторые значения:
| x | -2 | -1 | 1 | 2 |
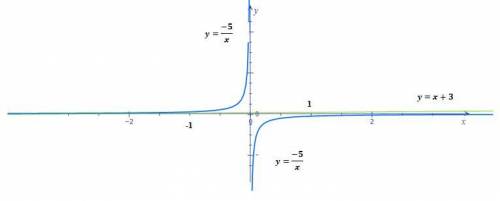
| y=-5/x | -5/2 | -5 | 5 | 5/2 |
| y=x+3 | 1 | 2 | 4 | 5 |
График функций в приложенном рисунке 2.
а. 50 м² Арман очистил за 10 минут
б. 15 пакетов потребуется, чтобы расфасовать 150 кг гречки по 10 кг в каждый
Пошаговое объяснение:
а. Одна сотка представляет собой квадрат 10 метров на 10 метров, следовательно, 1 сотка = 100 м²
Составим пропорцию:
100 м² - 20 минут
х м² - 10 минут
х = 100 * 10 : 20 = 1000 : 20 = 50 м² Арман очистил за 10 минут
б. 50 : 10 = по 5 (кг) гречки расфасовали в каждый пакет из 10.
150 : (5 + 5) = 150 : 10 = 15 (пакетов) потребуется, чтобы расфасовать 150 кг гречки по 10 кг в каждый