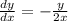
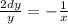 - уравнение с разделёнными переменными
- уравнение с разделёнными переменными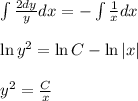
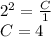
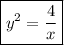 - частный интеграл.
- частный интеграл.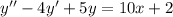
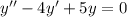
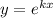 , тогда получаем
, тогда получаем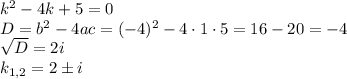
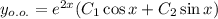
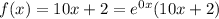
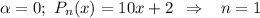
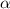 с корнями характеристического уравнения и принимаем во внимания что n=1, то частное решением будем искать в виде:
с корнями характеристического уравнения и принимаем во внимания что n=1, то частное решением будем искать в виде: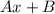
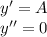
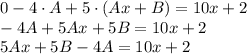
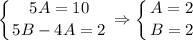
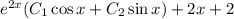
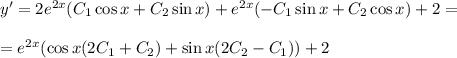
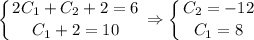
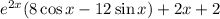
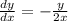
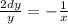 - уравнение с разделёнными переменными
- уравнение с разделёнными переменными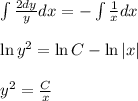
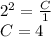
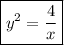 - частный интеграл.
- частный интеграл.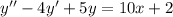
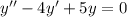
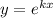 , тогда получаем
, тогда получаем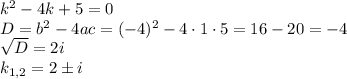
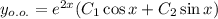
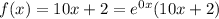
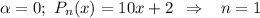
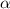 с корнями характеристического уравнения и принимаем во внимания что n=1, то частное решением будем искать в виде:
с корнями характеристического уравнения и принимаем во внимания что n=1, то частное решением будем искать в виде: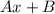
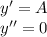
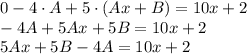
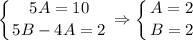
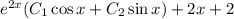
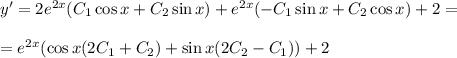
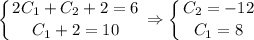
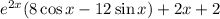
За те же 30 минут мальчик пройдёт в своём направлении 2 км.
Схематично изобразив передвижение мальчика и девочки, получим прямоугольный треугольник с катетами 2 и 1.5. Для того, чтобы найти расстояние между девочкой и мальчиком через 30 минут, нужно найти гипотенузу. (Теорема Пифагора)
a^2=4+2.25=6.25
a=2.5 км
ответ: 2,5 км.