Данный тип уравнений чаще всего называться дробным уравнением с одним параметром.
Решается он, очень легко. Все решение можно свести к такому плану:
Сводим уравнение к пропорции Умножаем крайние и средние члены, получив при этом еще одно уравнениеРешаем получившиеся уравнениеРазберем на практике:
1)
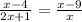
Здесь мы можем пропустить первый пункт нашего плана, так как уже имеем пропорцию¹.
Итак - как же решать пропорцию?.. Воспользуемся ее основным свойством²:
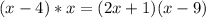
Перейдем к третьему пункту: Решим полученное уравнение. Для этого раскроем скобки³:
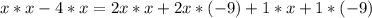
Сократим:
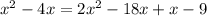
Теперь наша задача перенести значения в одну "сторону" (при этом следует не забывать изменять знак на противоположный):
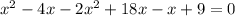
Сократим:
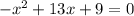
Получаем квадратное уравнение⁴. Решим его:
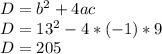
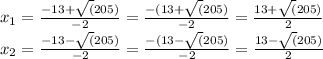
Это и есть два ответа.
2)
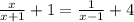
В этом же случае нам надо "воссоздать" пропорцию:
Добавим дроби и цифры⁵:
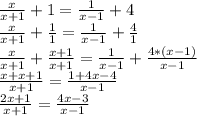
О чудо - получаем пропорцию! Переходим ко второму пункту (то же решение, что и в первом задании):
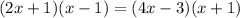
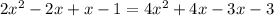
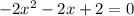
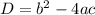

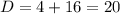
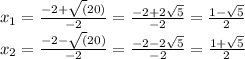
Это и есть два ответа.
(Решение остальных двоих примеров в прикрепленном файле, советую решить их самому и свериться со мной)
Удачной сессии! :)
_________________________
Пропорция¹ - отношение двух пар чисел: 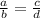 (что-то поделить на что-то, равно чему-то поделить на что-то). a и d - крайние члены, b и c - средние члены.
(что-то поделить на что-то, равно чему-то поделить на что-то). a и d - крайние члены, b и c - средние члены.
Основное свойство пропорции²:
Произведение крайних членов равно произведению средних членов.
Это значит, что если у нас есть пропорция 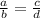 , то
, то 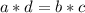 .
.
Как раскрываться скобки³:
Есть два типа уравнений, в которых нам понадобится раскрывать скобки в процессе решения подобных примеров:
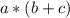
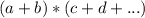
Сначала рассмотрим первый:
Наша задача поочередно умножить a на каждую переменную второй скобки:
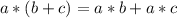
Теперь второй:
Тут наша задача такая же, но теперь мы умножаем сначала a на все переменные второй скобки, а потом b на все переменные второй скобки:
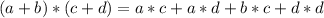
Квадратное уравнение⁴ - уравнение вида 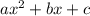 , где a, b и c - коэффициенты (цифры, стоящие перед x², x и без x вовсе).
, где a, b и c - коэффициенты (цифры, стоящие перед x², x и без x вовсе).
Решается квадратное уравнение обычно с соответственной формулы:
Для начала находится дискриминант (D) (такое значение, которое нам пригодится в бедующем):
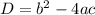
Затем используется формула (x₁ и x₂ - корни уравнения (решение)):
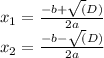
Как добавлять дроби и цифры⁵:
Имеем уравнение 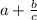 . Мы помним, что число, деленное на 1 равно самому себе (2 : 1 = 2, 3 : 1 = 3 и тд.). Также мы помним, что знак дроби означает деление. То есть получаем:
. Мы помним, что число, деленное на 1 равно самому себе (2 : 1 = 2, 3 : 1 = 3 и тд.). Также мы помним, что знак дроби означает деление. То есть получаем:
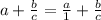
Теперь добавим две дроби, приведя их к общему знаменателю (знаменатель у двоих дробей должен быть одинаковым):
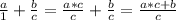
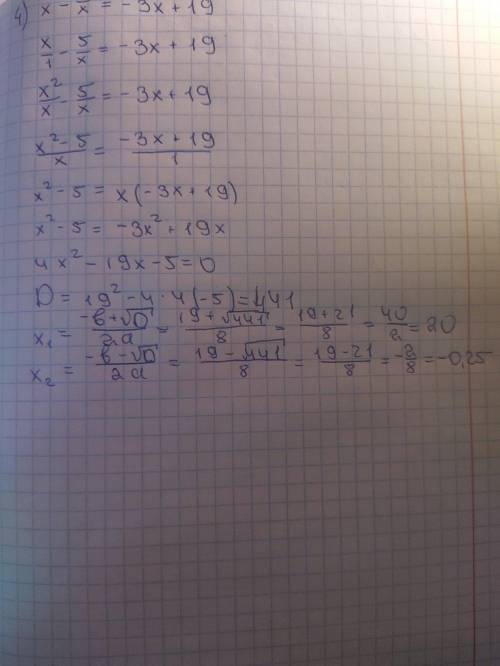
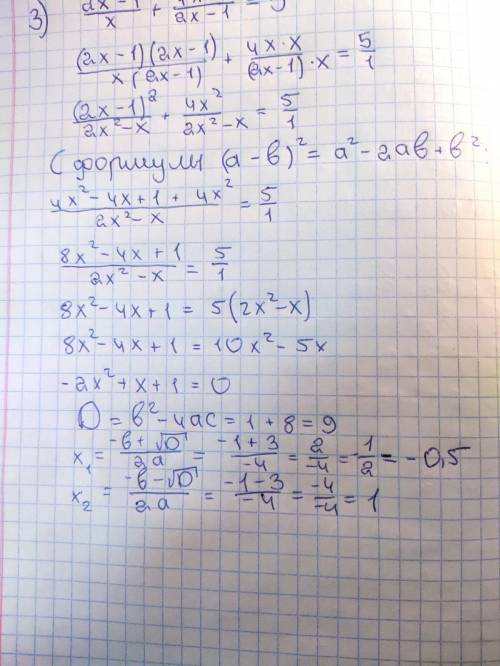
30=·2·3·5
40=2·2·2·5
2·3·5·2·2=120