ответ: 8π
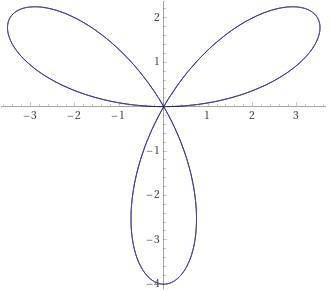
Пошаговое объяснение: r=4sin (3ф) это уравнение 3-х лепестковой розы в полярной системе координат.
Максимальное значение r=4, min r=0.
Период функции Sin (3ф)= 2π/3 Разделим на3 равные части лучами [0; 2π] в полярной системе координат, выполним рисунок (прилагается). Найдём площадь S₁ половины лепестка розы, а затем умножим на 6. Пределы интегрирования от 0 до π/6 ( у знака интеграла плохо видно)
S₁= 1/2·∫₀ⁿ⁾⁶(4sin(3ф))²dф= 1/2·∫₀ⁿ⁾⁶ 16sin²(3ф)dф=8·∫₀ⁿ⁾⁶sin²(3ф)dф=
4·∫₀ⁿ⁾⁶(1-сos(6ф)dф= 4·∫₀ⁿ⁾⁶dф - 4/6 ·∫₀ⁿ⁾⁶сos(6ф)d(6ф)=
=(4ф-sin(6ф))|₀ⁿ⁽⁶=2π/3 - sin(π)-0+0=2π/3
Значит S=6·S₁=6·(2π/3)=8π
Дано:
Весь путь=28 км
Проехал=1/4 часть пути (четверть пути)
Найти: Оставшийся путь=? км
Решение
1) Найдем сколько км проехал рыбак:
28*1/4=28/4=7 (км)
2) Вычислим сколько км осталось проехать рыбаку:
28-7=21 (км)
ответ: рыбаку осталось проехать 21 км.
или
Решим задачу с пропорции:
Весь путь равен 28 км и составляет 4/4 пути (1)
Рыбак проехал ¼ пути, значит ему осталось проехать 4/4-1/4=3/4 пути.
28 км – 1 часть
х км – ¾ части
х=28*3/4:1=28*3/4=7*3/1=21 км