Пусть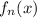 
означает 
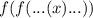, где 
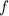применена 
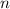раз.
Поскольку 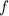многочлен, то у него есть значение в любой точке. (*)
Докажем утверждение по индукции.
База: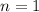 
- это то, что дано по условию.
Переход:
Пусть для некоторого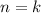 
верно; Докажем, что из этого следует справедливость утверждения и для 
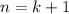; Действительно, по предположению индукции множество решений уравнения 
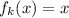совпадает с 
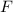; Возьмем 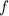от обеих частей (благодаря (*) мы можем это сделать): 
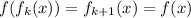; Но если сделать замену 
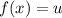, получим 
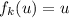; А множество решений этого уравнения лежит в 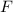; Предположим, что есть некоторый элемент 
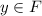, такой, что для него не найдется 
, чтобы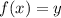 
; Тогда 
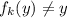, но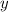 
лежит в 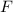, противоречие. Это завершает переход.
х + 2 = меньше 8
3день - х +4 = больше 8
х = 5
5+2 = 7 меньше 8
7 + 2= 9