Пошаговое объяснение:
Задача на комбинаторику.
В комбинаторике разделяют два типа задач: на сочетания и размещения.
Сочетание - это тип задач в комбинаторике, в которых порядок элементов не важен.
Размещение - это тип задач в комбинаторике, в которых порядок элементов важен.
У нас задача на размещение.
Формула для решения задач на размещения:
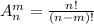
Где n - общее количество карт в колоде; m - количество вальтов; дам.
Подставляем значения в формулу:
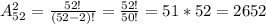
Напоминаю, что 52! это - 1 * 2 * 3 * 4 * 5 * 6 ... * 52.
Следовательно, 50! это - 1 * 2 * 3 * 4 * 5 * 6 ... * 50
52! и 50! можем сократить на 50!, в числителе останется 51 * 52, а в знаменателе - 1(мы числитель и знаменатель всегда можем домножить на единицу).
Получаем
Решаем пункт б:
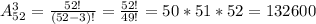
Все то же самое, что и в пункте а.
Задача решена.
Пошаговое объяснение:
Задача на комбинаторику.
В комбинаторике разделяют два типа задач: на сочетания и размещения.
Сочетание - это тип задач в комбинаторике, в которых порядок элементов не важен.
Размещение - это тип задач в комбинаторике, в которых порядок элементов важен.
У нас задача на размещение.
Формула для решения задач на размещения:
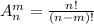
Где n - общее количество карт в колоде; m - количество вальтов; дам.
Подставляем значения в формулу:
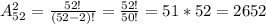
Напоминаю, что 52! это - 1 * 2 * 3 * 4 * 5 * 6 ... * 52.
Следовательно, 50! это - 1 * 2 * 3 * 4 * 5 * 6 ... * 50
52! и 50! можем сократить на 50!, в числителе останется 51 * 52, а в знаменателе - 1(мы числитель и знаменатель всегда можем домножить на единицу).
Получаем
Решаем пункт б:
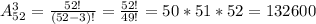
Все то же самое, что и в пункте а.
Задача решена.