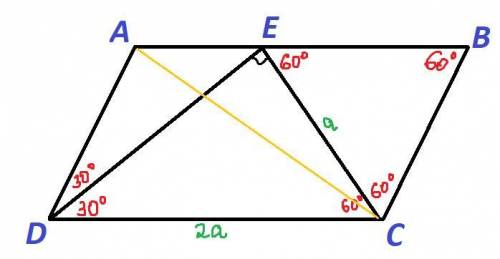
Так как угол ADC равен π/3, то есть 60°, и DE - биссектриса угла ADC, то углы ADE и CDE равны по 60°:2=30°.
Сумма смежных углов параллелограмма равна 180°, значит:
∠BCD=180°-∠ADC=180°-60°=120°
Так как угол BCD равен 120° и CE - биссектриса угла BCD, то углы BCE и DCE равны по 120°:2=60°.
Рассмотрим треугольник CDE. Так как два угла в нем известны, то найдем третий угол CED:
∠CED=180°-∠CDE-∠DCE=180°-30°-60°=90°
Значит, треугольник CDE - прямоугольный.
В прямоугольном треугольнике катет лежащий против угла в 30° равен половине гипотенузы.
Введем обозначения. Пусть катет CE, лежащий против угла в 30°, равен a. Тогда гипотенуза CD равна 2а. Заметим, что CD соответствует одной из сторон параллелограмма.
Рассмотрим треугольник ВСЕ. Найдем неизвестные его углы.
Так как противоположные углы параллелограмма равны, то:
∠ABC=∠ADC=60°
Зная два угла треугольника, найдем третий:
∠BEC=180°-∠BCE-∠CBE=180°-60°-60°=60°
Все углы треугольника ВСЕ равны, значит он - равносторонний.
Одна из сторон треугольника ВСЕ обозначена как а, значит и все его стороны равны а. В том числе, сторона параллелограмма ВС=а.
Таким образом, известны в наших обозначениях стороны параллелограмма: AB=DC=2a, BC=AD=a.
Рассмотрим треугольник АВС. Запишем для него теорему косинусов:
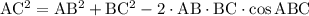
Подставим известные соотношения:
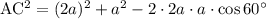
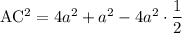
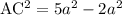
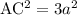
По условию АС=3.
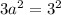
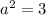
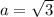(отрицательный корень смысла не имеет)
Вернемся к треугольнику CDE. Две стороны в нем теперь известны: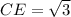 
, 
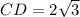. Запишем теорему Пифагора:
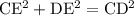
Выражаем искомый отрезок DE:
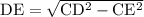
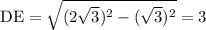
ответ: 3
Всего 6 рисунков
Пошаговое объяснение:
Число различных рисунков есть то же самое, что и количество различных сочетаний (перестановок) групп по три из трех.
Всего таковых насчитывается 3! (читается как три факториал, а считается как произведение всех натуральных чисел от одного до в данном случае трех)
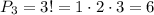
Кратко докажем что это так:
Будем закрашивать в конкретном порядке:
(голова(Г) -> крылья(К) -> хвост(Х))
Г - закрашиваем любыми цветами - их 3
К - закрашиваем любым из оставшихся - их 2
Х - закрашиваем единственным оставшимся - он 1
Отсюда и число сочетаний
Для каждого из 3 разных варианта Г есть по 2 варианта К (мы ведь уже использовали одну краску, т.е. две осталось); итого 3*2=6 вариантов.
И для каждого из 6 вариантов существует по единственному варианту Х (две краски из трех ведь мы использовали)
Итого и получаем 3*2*1 = 1*2*3 = 3! = 6 вариантов рисунков всего
