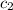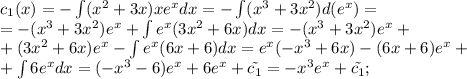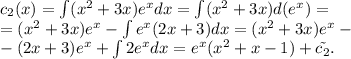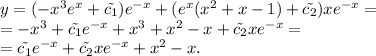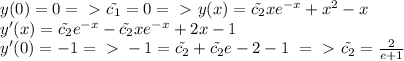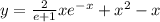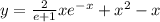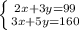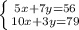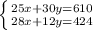Какие права можно придумать для детей например ребёнок имеет право только свои придумайте надо учительница прибьет : (: (: (: (: (: (: (: (: (: (: (: (: (: (: (: (: (: (: (: (: (: (: (: (: (: (: (: (: (: (: (: (: (: (: (: (: (: (: (: (: (: (: (: (: (: (: (: (: (: (: (: (: (: (: (: (: (: (: (: (: (: (: (: (: (: (: (: ( только свои не из !
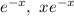
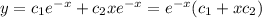
![y(x)=e^{-x}[c_1(x)+xc_2(x)]](/tpl/images/0409/7136/59e14.png)
![y'(x)=-e^{-x}[c_1(x)+xc_2(x)]+e^{-x}[c_1(x)+xc_2(x)]'= \\ =-e^{-x}[c_1(x)+xc_2(x)]+e^{-x}[c_1'(x)+c_2(x)+xc_2'(x)]= \\ = -c_1(x)e^{-x}-c_2(x)xe^{-x}+c_1'(x)e^{-x}+c_2(x)e^{-x}+c_2'(x)xe^{-x}= \ \textgreater \ \\ =\ \textgreater \ c_1'(x)e^{-x}+c_2'(x)xe^{-x}=0\\ \\ y'(x)=-c_1(x)e^{-x}-c_2(x)xe^{-x}+c_2(x)e^{-x}](/tpl/images/0409/7136/b3480.png)
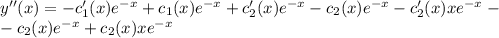
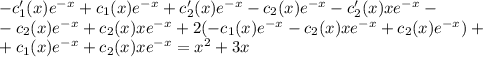
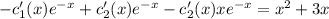
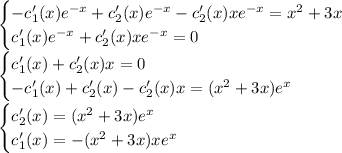
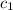 и
и