3/12 + 25/30 = 1 1/12(одна целая одна двенадцатая )
30/54+22/30= 1 13/45(одна целая тринадцать сорок пятых)
12/27+14/21 = 1 1/9 (одна целая одна девятая)
12/18-5/60=7/12
1/5+1/9+1/3=29/45
5/6+3/8-1/4=23/24
1/3+4/9+5/6==2
/-это дробная черта
Пошаговое объяснение:
3/12 + 25/30 =5*3/5*12 + 2*25/2*30 = 15/60 +50/60 = 65/60 =13/12= 1 1/12(одна целая одна двенадцатая )
30/54+22/30= 5*30/5*54 + 9*22/9*30 =150/270+ 198/270 =348/270 = 348:6/270:6=58/45= 1 13/45(одна целая тринадцать сорок пятых)
12/27+14/21 =7*12/7*27 =9*14/9*21= 84/189+126/189=210/186= 10/9 = 1 1/9 (одна целая одна девятая)
12/18-5/60=10*18/10*18 – 5*3/60*3=120/180-15/180=105/180=7/12
1/5+1/9+1/3=1*9+1*5+1*15/45=9+5+15/45=29/45
5/6+3/8-1/4=5*4+3*3-1*6/24=20+9-6/24=23/24
1/3+4/9+5/6=1*6+4*2+3*6/18=6+8+18/18=32/18=2
/-это дробная черта
120
Пошаговое объяснение:
Пусть Саша выбрал число a, Андрей - число b, Оля - число c. Опишем последовательность действий.
1) Саша умножил своё число на каждое из других, получилось ab и ac. Затем вычел меньшее из большего. Тогда получается выражение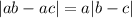 
. a можно вынести за модуль, так как оно натуральное.
2) Аналогично, у Андрея получилось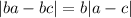 
.
У Оли получилось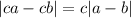 
3) По условию,
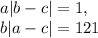
Из первого равенства можно получить два варианта:
а)
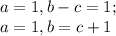
б)
,
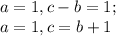поскольку 1 можно разложить на натуральные множители лишь
Рассмотрим второе равенство и подставим туда каждый случай из первого:
а)
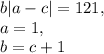
Отсюда:
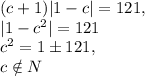
б)
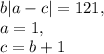
Отсюда:
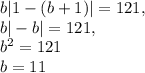
Далее находим c: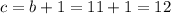 
Однозначно определяем число Оли: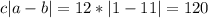 
Раскладываем знаменатель последней дроби на множители, для этого решаем квадратное уравнение:
х2+9х+20 =0
Д=81-80=1
х(1)=-4
х(2)=-5
х2+9х+20=(х+4)(х+5)
1/(х+3)(х+4) + 1/(х+3)(х+5)+ 1/(х+4)(х+5) ≥1
приводим к общему знаменателю ( х+3)(х+4)(х+5) и отбрасываем его , заметив, что х≠-3, х≠-4, х≠-5
(х+5) + (х+4) + (х+3) ≥ ( х+3)(х+4)(х+5)
х3 + 12 ≥ (х2+7х+12)(х+5)
х3 + 12 ≥ х3+5х2+7х2+35х+12х+60
12х2+47х+48≤0
12х2+47х+48=0
Д= 2209 - 2304 <0 нет корней
Парабола ветви вверх, целиком лежит выше оси х, значит
ответ: {пустое множество}