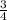 переведем в неправильную дробь, для этого нужно 1*4+3=7, значит вся дробь теперь
переведем в неправильную дробь, для этого нужно 1*4+3=7, значит вся дробь теперь 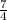 (целую часть умножаем на знаменатель, затем прибавляем к числителю. Получившееся число записываем в числитель, знаменатель без изменений)
(целую часть умножаем на знаменатель, затем прибавляем к числителю. Получившееся число записываем в числитель, знаменатель без изменений)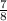 • х =
• х = 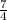
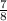
 в неправильную, получается
в неправильную, получается 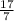
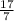 =
=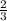
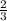 :
: 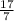
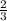 •
• 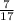
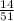
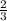 в неправильную дробь, получится
в неправильную дробь, получится 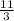
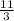 •
• 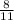
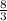
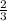
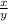 =
=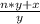
4 целых 2/25 = 102/25 = 4,08