Т.к. случайная величина X может принимать только два значения, то
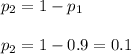
Математическое ожидание дискретной случайной величины равно сумме произведений значений этой величины на соответствующие вероятности
![M[X]=\sum\limits_{i=1}^{N}\,{x_i\,p_i}](/tpl/images/2004/8694/e38e8.png)
Для данной задачи
![M[X]=x_1\,p_1+x_2\,p_2](/tpl/images/2004/8694/1be08.png)
Дисперсия дискретной случайной величины равна разности суммы произведений квадратов значений этой величины на соответствующие вероятности и квадрата математического ожидания
![D[X]=\sum\limits_{i=1}^{N}\,{x_i^2\,p_i}-(M[X])^2](/tpl/images/2004/8694/0b48e.png)
Для данной задачи
![D[X]=x_1^2\,p_1+x_2^2\,p_2-(M[X])^2](/tpl/images/2004/8694/6c44c.png)
Имеем 2 уравнения с двумя неизвестными величинами. Составим и решим систему уравнений
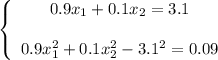
Решением данной системы являются 2 пары значений
Первая пара значений:
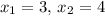
Закон распределения
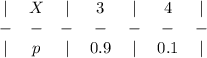
Вторая пара значений
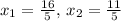
Закон распределения
Вершины ∆АВС имеют координаты: А(-2; 0; 1), В(-1; 2; 3), С(8; -4; 9). Находим:
а) координаты и длину вектора AB.
AB=(-1-(-2); 2-0; 3-1) = (1; 2; 2),
|AB| = √(12 + 22 + 22) = √(1 + 4 + 4) = √9 = 3.
б) периметр ∆АВС.
BC = (8-(-1); -4-2; 9-3) = (9; -6; 6),
|BC| = √(92 + (-6)2 + 62) = √(81 + 36 + 36) = √153.
AC = (8-(-2); -4-0; 9-1) = (10; -4; 8),
|AC| = √(102 + (-4)2 + 82) = √(100 + 16+ 64) = √180 = 6√5.
P = 3 + √153 + 6√5 ≈ 28,78572.
в) угол А.
Используем найденные векторы АВ и АС и их модули:
AB = (1; 2; 2), |AB| = 3.
AC = (10; -4; 8), |AC| = 6√5.
cos A = (1*10 + 2*(-4) + 2*8) / (3*6√5) = 16 / (18√5) = 8 / (9√5) ≈ 0,447214.
Угол А = arc cos(8/9√5) = 1,10715 радиан или 63,43495 градуса.
г) координаты точки М - середины ВС.
М = (В( -1; 2; 3 ) + С( 8; -4; 9 ))/2 = (3,5; -1; 6).
д) длину медианы АМ. Точка А(-2; 0; 1)
АМ = (3,5 – (-2); -1-0; 6-1) = (5,5; -1; 5).
Длина (модуль) АМ равен:
АМ = √(5,52 + (-1)2 + 52) = √(30,25 + 1 + 25) = √56,25 = 7,5.
k є Z
===========================
k є Z
===========================
k є Z