ответ: 1,5 ч ; 2 ч
Пошаговое объяснение:
Пусть на первый участок мотоциклист затратил х часа , тогда на второй участок он затратил ( х + 0,5 ) часа. На первом участке он проехал 42х км , а на втором 30 ( x + 0.5 ) км . Так как всего он проехал 123 км , составим уравнение : 42x + 30 ( x + 0.5 ) = 123 42x +30x + 30 x 0.5 = 123 72x + 15 = 123 72x = 123 - 15 72x = 108 x = 108 : 72 x = 1,5 (ч ) мотоциклист проехал первый участок 1,5 + 0,5 = 2 (ч) проехал второй участок
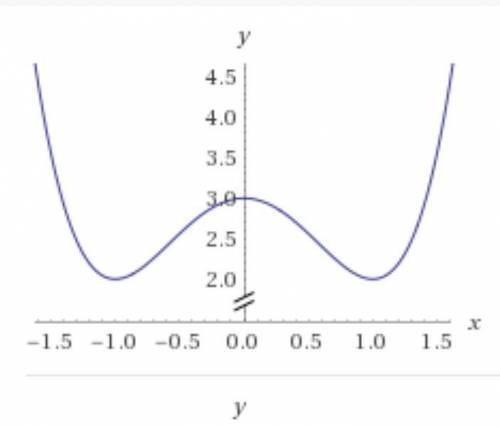
Дана функция f(x)=x^4 - 2x² + 3.
Её производная равна f(x) = 4x^3 - 4x = 4x(x² - 1).
Приравняв производную нулю, получаем 3 критические точки: х = 0 и х = +-1.
Находим знаки производной на промежутках (-∞; -1), (-1; 0), (0; 1), (1; ∞).
x = -2 -1 -0,5 0 0,5 1 2
y' = -24 0 1,5 0 -1,5 0 24 .
В точках х = +-1 есть 2 общих минимума, у(мин) = 2,
в точке х = 0 местный максимум.
Так как функция чётная, то на заданном промежутке максимальное значение функции в точке х = -4.
у = (-4)^4 - 2*(-4)² + 3 = 227.