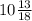
Пошаговое объяснение:
Прежде всего нужно перевести периодическую дробь в обыкновенную. В смешанных периодических дробях между запятой, отделяющей целую часть от дробной, и периодом могут присутствовать другие цифры. Смешанные периодические дроби следуют немного другим законам перевода в обыкновенные. Количество знаков в знаменателе остается равным количеству знаков после запятой, включая в период, но теперь знаменатель будет состоять не только из 9, но и из 0, где количество 9 – это количество цифр в периоде, а количество 0 – это количество цифр между запятой и периодом. Числитель же рассчитывается через разность числа записанного после запятой, включая период, и числа, представляющего набор цифр между запятой и периодом.
Целое число мы не трогаем, оставляем как есть, работаем только с дробью после запятой:
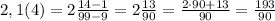
Итак, 20 процентов от некоего числа равны 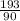
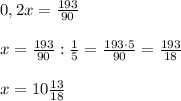
Что и требовалось доказать.
Пошаговое объяснение:
1)АС - общая для обоих треугольников. Значит эти треугольники равны, т.к. у них равны две стороны и углы между ними.
2)Углы АОК и ВОС - вертикальные, значит они равны. Из этого следует, что треугольники равны по тому же признаку, что и в первой задаче.
3)Тут уже всё дано. Треугольники равны по тому же признаку, что в 1 и 2 задачах.
4)Если углы АКО и КОМ равны, то их смежные углы тоже будут равны. Тогда угол СКА равен углу МОЕ. Исходя из этого, треугольники равны по двум сторонам и углам между ними.
6)АВСD - параллелограмм. Тогда АВ = CD. BD - общая для обоих треугольников. Значит треугольники равны по двум сторонам и углам между этими сторонами.
480 : 60 = 8 часов будет заполняться бассейн