ответ: исходное неравенство верно при любых х, если
{2-m< 0
{d< 0
{m> 2 {m> 2
{4m² - 4*(2-m)²< 0; {(2m-4+2m)(2m+4-2m)< 0
{m> 2 {m> 2
{16(m-1)< 0 {m< 1
нет таких m.
при 2-m=0 откуда m=2 имеется -4x< 0 ⇒ x> 0 ( это нам не подходит)
ответ: нет таких m.

1) Если х < 0, то левая часть неотрицательна в силу модуля, правая - отрицательна. Верно всегда, в ответ. 2) Если х = 0, то 30 >= 0 - верно. 3) Если х > 0, то можно возвести обе части в квадрат и представить это в виде разности квадратов:
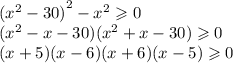
Методом интервалов при х > 0: х принадлежит (0;5] U [6; + беск.)
В итоге получаем ответ: ( - беск. ; 5 ] U [ 6 ; + беск. ). Не являются решением данного неравенства х принадлежит (5;6), но в этот интервал не входят целые числа, поэтому их количество равно 0
ответ: 0.
30 : 3 = 10 копеек - вторая торговка
15 + 10 = 25 копеек - вместе
(60 : 5 ) * 2 = 24 копейки - они выручили меньше на 1 копейку