Вид стрички завдожки 5м видризали три шматки по 6 дм.яка завдожки стричка залишилася?

👇

Увидеть ответ

Ответ:

LollyMelor

26.11.2021

3*6=18 дм.
500-180=320 = 3 м. 2 дм.

4,7(33 оценок)

Ответ:

Саша99990

26.11.2021

5 М=50 ДМ 3*6=18дм 50-18=32дм або 3м2дм

4,7(52 оценок)

Открыть все ответы

Ответ:

makrona123

26.11.2021

1) Находим первую производную функции:
y' = -3x²+12x+36
Приравниваем ее к нулю:
-3x²+12x+36 = 0
x₁ = -2
x₂ = 6
Вычисляем значения функции на концах отрезка
f(-2) = -33
f(6) = 223
f(-3) = -20
f(3) = 142
ответ:   fmin = -33, fmax = 142
2)
a) 1. Находим интервалы возрастания и убывания.
Первая производная равна
f'(x) = - 6x+12
Находим нули функции. Для этого приравниваем производную к нулю
- 6x+12 = 0
Откуда:
x₁ = 2
(-∞ ;2)   f'(x) > 0   функция возрастает
(2; +∞) f'(x) < 0функция убывает
В окрестности точки x = 2 производная функции меняет знак с (+) на (-). Следовательно, точка x = 2 - точка максимума.
б) 1. Находим интервалы возрастания и убывания. Первая производная.
f'(x) = -12x2+12x
или
f'(x) = 12x(-x+1)
Находим нули функции. Для этого приравниваем производную к нулю
12x(-x+1) = 0
Откуда:
x1 = 0
x2 = 1
(-∞ ;0)   f'(x) < 0 функция убывает
(0; 1)   f'(x) > 0   функция возрастает
(1; +∞)   f'(x) < 0   функция убывает
В окрестности точки x = 0 производная функции меняет знак с (-) на (+). Следовательно, точка x = 0 - точка минимума. В окрестности точки x = 1 производная функции меняет знак с (+) на (-). Следовательно, точка x = 1 - точка максимума.

3. Исследуйте функцию с производной f(x)=2x^2-3x-1
1. D(y) = R
2. Чётность и не чётность:
f(-x) = 2(-x)² - 3*(-x) - 1 = 2x² + 3x - 1 функция поменяла знак частично. Значит она ни чётная ни нечётная
3. Найдём наименьшее и наибольшее значение функции
Находим первую производную функции:
y' = 4x-3
Приравниваем ее к нулю:
4x-3 = 0
x₁ = 3/4
Вычисляем значения функции
f(3/4) = -17/8
Используем достаточное условие экстремума функции одной переменной. Найдем вторую производную:
y'' = 4
Вычисляем:
y''(3/4) = 4>0 - значит точка x = 3/4 точка минимума функции.
4. Найдём промежутки возрастания и убывания функции:
1. Находим интервалы возрастания и убывания.
Первая производная равна
f'(x) = 4x-3
Находим нули функции. Для этого приравниваем производную к нулю
4x-3 = 0
Откуда:
x₁ = 3/4
(-∞ ;3/4)   f'(x) < 0 функция убывает
(3/4; +∞)   f'(x) > 0   функция возрастает
В окрестности точки x = 3/4 производная функции меняет знак с (-) на (+). Следовательно, точка x = 3/4 - точка минимума

4,7(20 оценок)

Ответ:

Sonya121s

26.11.2021

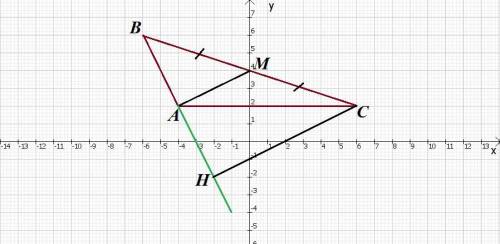
По чертежу (рис. 1) мы замечаем, что AM || CH, но для полного убеждения, составим функции прямых по формуле y = kx + m и решим систему уравнений.

Возьмём две любые точки (желательно брать такие точки, если они есть, чтобы аргумент (х) был равен 0; тогда пропадёт коэффицент k и найти m будет легче) для AM, например, (0; 4) и (-2; 3). Составляем таблицу:

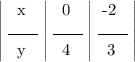
$\left|\;{\begin{array}{}\;\;x\\\line(1,0)9\line(1,0)9\\\;\;y\end{array}\;\right|\left\begin{array}{}\;\;0\\\line(1,0)9\line(1,0)9\\\;\;4\end{array}\;\right|\left\begin{array}{}\;-2\\\line(1,0)9\line(1,0)9\\\;\;3\end{array}\;\right|$

Теперь данные из таблицы подставляем к линейной функции вида

y = kx + m:

4 = k0 + m

4 = m ⇒ y = kx + 4

Теперь, находим коэффицент k:

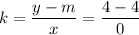$k=\dfrac{y-m}x=\dfrac{4-4}0$ , на 0 делить нельзя, поэтому берем другие точки

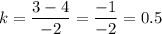
$k=\dfrac{3-4}{-2}=\dfrac{-1}{-2}=0.5$

Получаем линейную функцию y = 0,5x + 4

Аналогично действуем для второй прямой

1) Таблица:

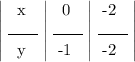
$\left|\;{\begin{array}{}\;\;x\\\line(1,0)9\line(1,0)9\\\;\;y\end{array}\;\right|\left\begin{array}{}\;\;0\\\line(1,0)9\line(1,0)9\\\;-1\end{array}\;\right|\left\begin{array}{}\;-2\\\line(1,0)9\line(1,0)9\\\;-2\end{array}\;\right|$

2) Подставляем значения в y = kx + m:

-1 = k0 + m

-1 = m ⇒ y = kx - 1

3) Находим k:

Так как прямые параллельны, то k будет одинаковый (можно проверить):

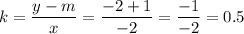
$k=\dfrac{y-m}x=\dfrac{-2+1}{-2}=\dfrac{-1}{-2}=0.5$

⇒ y = 0,5x - 1

Наконец, составляем систему уравнений

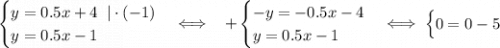
$\begin{cases}y=0.5x+4\;\;|\cdot(-1)\\y=0.5x-1\end{cases}\Longleftrightarrow\;\;\;+\begin{cases}-y=-0.5x-4\\y=0.5x-1\end{cases}\Longleftrightarrow\;\begin{cases}0=0-5\end{cases}$