6
Пошаговое объяснение:
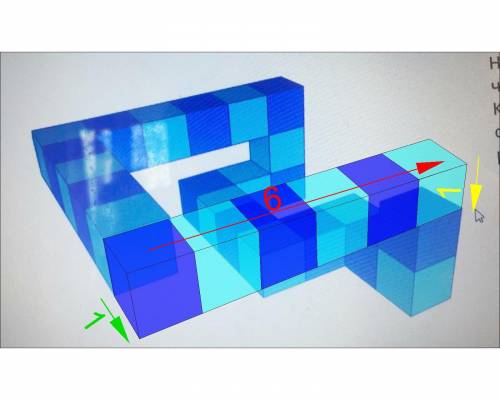
Для правильного решения задания нужно внимательно рассмотреть рисунок и поочерёдно просчитать смещение относительно начального кубика в трёх направлениях.
На первом рисунке показаны смещение вдоль оси z - жёлтым цветом, вдоль оси у - зелёным цветом, вдоль оси х - красным цветом.
Посчитаем, как сместилась конечная точка от начальной:
х: -3+3-6 = -6
у: 2+4-5 = 1
z: -2+3 = 1.
Значит нужно из конечной точки сместиться на:
-1 вдоль оси у,
+6 вдоль оси х,
-1 вдоль оси z.
На втором рисунке мы видим что смещение на -1 вдоль оси у и -1 вдоль оси z обеспечивается стыковкой горизонтальной полосы из 6 кубиков, которые дают смещение на +6 вдоль оси х.

Випишемо координати початку O і кінця A вектора a:
O(0;0), A(1;3).
Обчислимо координати вектора a як різницю координат кінця A(1;3) та початку O(0;0):
A(1-0;3-0)=(1;3).
Пошаговое объяснение:
Обчислимо довжину (модуль) вектора a(1;3):
довжина вектора
Такі ж операції проводимо для вектора с:
O(0;0), C(3;1).
Координати вектора c знаходимо через різницю координат кінця C(3;1) та початку O(0;0):
c(3-0;1-0)=(3;1).
Через корінь квадратний з суми квадратів координат знаходимо довжину (модуль) вектора c(3;1):
модуль вектора
Скалярний добуток векторів a(1;3) і c(3;1):
a•c=1•3+3•1=6.
92у=33.267+12.917
92у=46.184
у=46.184:92
у=0.502