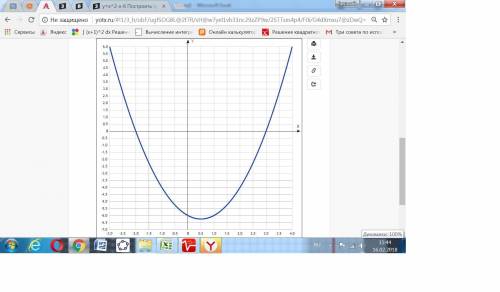
График функции y=x^2-x-6 это парабола ветвями вверх.
Найдём координаты её вершины.
Хо =-в/2а = -(-1)/(2*1) = 1/2.
Уо = (1/4)-(1/2)-6 = -6,25.
Определяем точки пересечения с осями.
С осью Оу при х = 0 у = -6.
С осью Ох при у = 0 надо решить уравнение x^2-x-6 = 0.
Квадратное уравнение, решаем относительно x: Ищем дискриминант:
D=(-1)^2-4*1*(-6)=1-4*(-6)=1-(-4*6)=1-(-24)=1+24=25;Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(√25-(-1))/(2*1)=(5-(-1))/2=(5+1)/2=6/2=3;x_2=(-√25-(-1))/(2*1)=(-5-(-1))/2=(-5+1)/2=-4/2=-2.
Имеем 2 точки пересечения оси Ох: х = -2 и х = 3.
Можно найти ещё несколько точек для точного построения.
Так как парабола имеет ось симметрии х = 1/2, то можно определить точки справа от оси, потом построить им симметричные.
х = 2, у = 4 - 2 - 6 = -4,
х = 4, у = 16 - 4 - 6 = 6.
Пошаговое объяснение:
в)4х^2-16=0
4x^2=16\
x^2=4
x=2 , x=-2
г)x^2-2x-8=0
d^2=2^2+4*8=36 d=6
x1=2+6/2*1 x=4
x2=2-6/2*1=-2
ответ -2 , 4
2. Пусть длина одной из сторон равна x. Тогда длина второй стороны равна (62 - 2x)/2 (надеюсь, понятно почему) .
Записываем уравнение:
x * (62 - 2x)/2 = 210
Преобразовываем:
62x - 2x^2 = 420
x^2 - 31x + 210 = 0
Дискриминант:
D = 31^2 - 4*210 = 961 - 840 = 121 = 11^2
x = (31 +- 11)/2
21 и 10 см.
3.Подставляем на место х один из известных корней
4^2+4р-12=0
16+4р-12=0
4+4р=0
4р=-4
р=-1
Подставляем полученное значение р и находим второй корень
х^2-х-12=0
Д=1+48=49
х1,2= (1+-7)/2
х1=1+7/2=4
х2=1-7/2=-3
ответ: р=-1, х2=-3
2)92-23=69 рублей - осталось после покупки книги
3)69: 1/3= 23 рубля - стоит набор для черчения