Пошаговое объяснение:
Предисловие
В настоящем сборнике собраны задачи по основным разделам теории вероятностей. Сборник разбит на восемь тем в соответствии
с изучаемой вероятностной моделью (основания теории, классическая схема, геометрические вероятности, схема Бернулли) или
применяемым математическим аппаратом (условные вероятности,
независимость событий, случайные величины и их распределения,
математическое ожидание, характеристические функции). Каждая тема содержит подробный теоретический материал, а также
большое количество примеров решения задач. Часть задач для
самостоятельного решения помещена в теоретический блок каждой темы, чтобы подчеркнуть их важность в освоении изучаемого материала. Номера обязательных задач подчеркнуты. Решение
сложных задач (со звездочкой и галочкой) будет
не только более глубокому пониманию существа методов теории
вероятностей, но и повышению рейтинговой оценки студента.
Символы греческого алфавита, а также готический шрифт написания латинских символов приведены в конце задачника.
Для более детального ознакомления с теоретическим материалом рекомендуем обратиться к следующим учебным пособиям;
ссылки на эти пособия приведены в начале каждой темы.
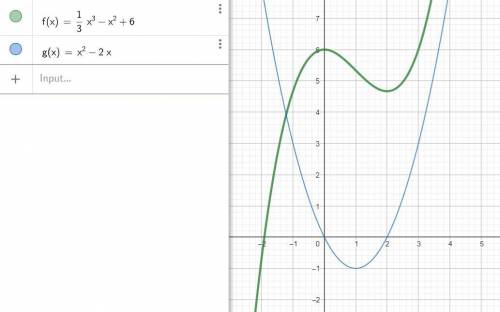
см. рис.
Пошаговое объяснение:
кубическая парабола,
снизу-вверх,
сплюснутая по вертикали в 3 раза
Взять производную,
исследовать f'(x) на f'(x) < 0, f'(x) > 0
определить экстремумы.
f'(x) = x² - 2x = x(x-2)
f'(x) = 0 при
x1 = 0
x2 = 2
f'(x) = x² - 2x (роги вверх => меньше нуля - между корнями)
f'(x) < 0 при x ∈ (0; 2) => f(x) убывает
f'(x) > 0 при x ∈ (-∞; 0) ∪ (2; +∞) => f(x) возрастает
х1 = 0 - точка максимума
х2 = 2 -точка минимума
считаем точки экстремумов
f(0) = 6
f(2) = 8/3 - 4 + 6 = 2+2/3 +2 = 4+2/3
дальше строим график, если руками - то считаем точки и соединяем плавной кривой.
В нашем случае благоприятный исход один, так как существует ровно выбрать 3 девушки из 3 возможных. Число всех исходов - число выбрать каких-то 3 человек из 10 возможных, оно равно 10*9*8/3*2*1=120 (порядок выбора не важен). Таким образом, вероятность равна 1/120.