Число будет делиться на 99, если оно делится на 9 и на 11.
Признак делимости на 9: необходимо, чтобы сумма цифр числа делилась на 9. Сумма известных цифр числа: 6 + 2 + 4 + 2 + 7 = 21. Таким образом, неизвестные цифры числа должны составлять в сумме 6 или 15. Например 3 и 3 или 8 и 7.
Признак делимости на 11: необходимо, чтобы сумма цифр числа, стоящих на четных местах, равнялась сумме цифр числа, стоящих на нечетных местах, или отличалась от нее на 11 в любую сторону.
Считаем цифры, стоящие на четных местах: 2 + 2 + х = 4 + х
На нечетных местах: 7 + 4 + у + 6 = 17 + у
Тогда:
4 + х + 11 = 17 + у
15 + х = 17 + у
Учитывая, что сумма х и у должна равняться или 6, или 15, получим:
х = 4; у = 2
Итоговое чило: 6224427 : 99 = 62873
ответ: 6224427
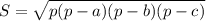 (1)
(1)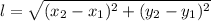 (2)
(2)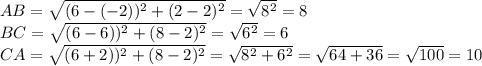
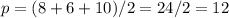
4-6х-12=3-5х
-6х+5х=3-4+12
-х=11
х=-11
Б)(5х+8)-(8х+14)=9
5х+8-8х-14=9
5х-8х=9-8+14
-3х=15
х=15:(-3)
х=-5
В)2,7+у=9*(у-2,1)
2.7+у=9у-18.9
у-9у=-18.9-2.7
-8у=-21.6
у=-21.6:(-8)
у=2.7
Г)0,3*(8-3у)=3,2-0,8*(у-7)
2.4-0.9у=3.2-0.8у+5.6
-0.9у+0.8у=3.2+5.6-2.4
-0.1у=6.4
у=6.4:(-0.1)
у=-64
Д)5/6*(1/3х-1/5)=3х+3 1/3
5\18х-1\6=3х+10\3
5\18х-3х=10\3+1\6
5\18х-54\18х=20\6+1\6
-49\18х=21\6
х=21\6*(-18\49)
х=-9\7
х=-1 2\7