1) Коробка прямоугольной формы - это прямой параллелипипед. Пусть a,b,c - линейные измерения прямоугольной коробки. Тогда по условию задачи
S₁=ab=5
S₂=bc=12
S₃=ac=15
(решение во вложении)
2) Пусть x- количество лет старшего брата и он старше младшего брата на y лет . Тогда младшему брату (x-y) лет
Когда старшему брату было (x-y) лет, то младшему было (x-y)-y=x-2y лет
Из условия задачи имеем уравнение
x-y=3*(x-2y)
Когда младшему брату будет x лет, старшему будет x+y лет
Составляем второе уравнение
x+(x+y)=60
Имеем систему
x-y=3x-6y
2x+y=60
2x-5y=0
2x+y=60
Из второго уравнения вычтем первое
6y=60
y=10 - разность в годах
2x+y=60 2x=60-y=50 x=25
То есть старшему брату 25 лет, а младшему 25-10=15 лет
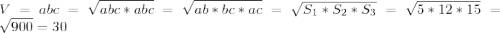
тут будем решать неравенством
пусть х тетрадь в линейку тогда по условию максимально возможное количество тетрадей в клетку х+9 нам известно что тетрадь в линейку стоит 2 коп а тетрадь в клетку 3 коп тогда стоимость каждого наименования будет 2х и 3(х+9) нам известно что у покупателя 1 руб и 40 коп иначе 140 коп соответственно сумма стоимости наименований не более имеющих денег
получаем
3(х+9)+2х≤140
3х+3×9+2х≤140
3х+27+2х≤140
5х+27≤140
5х≤113
х ∈ (-∞; 22.6]
так как количество может измерятся только в натуральных числах то ищем ближайшее целое число к 22,6 это 22 соответственно 22 тетрадок в линейку ⇒ 22+9=31 тетрадок в клетку
ответ: 22 тетрадок в линейку и 31 тетрадок в клетку
б)232+160=392дет-за 8 ч.
392:8=49дет-за 1 ч.
в)1176:49=за 24ч-изготовит 1176дет.
24:8=3 дня-понадобится.