49 см²
Пошаговое объяснение:
Вариант 1
Площадь прямоугольника - 14*7=98см²
Площадь прямоугольного треугольника считается по формуле =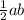 
где a и b - катеты.
Катеты треугольников ABS и CDU равны 7 и 7 см (точки S и U - середина, значит катеты CU и AS равны 7 см).
Отсюда площадь треугольника = 
= 24.5 см²
Площадь двух треугольников = 24.5*2=49 см²
Значит площадь заштрихованной фигуры = 98-49=49 см²
Вариант 2 (в качестве альтернативного решения)
т.к. точки U и S - середина, то образуются квадратыUCDS и BUSA со стороной 7 см. Т.к. треугольники занимают ровно половину квадратов, то получаем:
площадь квадрата - 7*7=49см²
из них заштрихованная = 49/2=24,5см²
Площадь двух заштрихованных областей - 24,5*2=49см²
Площадь сектора равна 1/6 площади круга
Площадь круга
S круга = пr^2 = 3,14 • 12^2 = 452,16 кв.см
S сектора =1/6(пr^2),
S сектора = (3,14•12^2)/6=75,36 кв.см
Вычислим площадь треугольника, составляющего 1/6 часть шестиугольника. Для этого проведем из вершины треугольника высоту h. Высота в равностороннем треугольнике делит основание пополам. Вычислим высоту как катет прямоугольного треугольника, в котором катет равен 6 см, а гипотенуза 12 см
h=корень из (12^2 - 6^2)= корень из (144-36)= корень из(108)
h примерно равна=10,39 см
Площадь треугольника равна половине произведения высоты на длину основания
S треуг.=12.•10,39/2=62,34 кв.см
Если из площади сектора вычесть площадь треугольника, то получим площадь сегмента, отрезанного стороной шестиугольника от круга
S сегмента = S сектора - S треуг, = 75,36-62,34=13,02 кв.см
Площадь круга равна 452,16 кв,см
Значит, площадь большей части круга на которые его делит сторона шестиугольника, равна площади круга без сегмента
S большей части круга = S круга - S сегмента = 452,16-13,02=439,14 кв.см