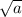, то необходимо домножить и числитель, и знаменатель на этот корень (основное свойство дроби)
или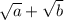 
, то числитель и знаменатель необходимо домножить на сопряжённое выражение (для первого: на 
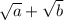; для второго выражения на 
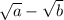), сведя числитель к формуле разности квадратов. Это алгоритм для квадратных корней. Для корней больше 2 степени сопряжённые ищутся иначе и по другим формулам.
![2x+1=y^3\\y= \sqrt[3]{2x+1}](/tpl/images/0179/7261/4c476.png)
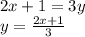
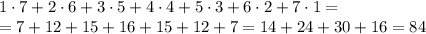
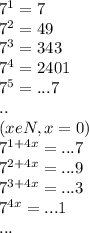
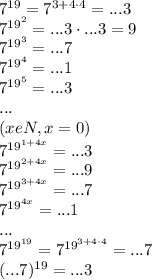
12. См. рис.
13. Пусть одно число x, другое 18-x, причём x > 18-x. Тогда по условию задачи.
10 < x-(18-x) < 14
10 < x-18+x < 14
10+18 < 2x < 14+18
28 < 2x < 32
14 < x < 16
x может быть равен только 15, т.к. числа натуральные. Одно число 15, второе 18-15 = 3.