A (4;2) ; B (-8;5)
1) Воспользуемся формулой нахождения координат вектора: вектор AB = {x₂-x₁ ; y₂-y₁}
Для удобства сделаем так: A (x₁;y₁) B (x₂;y₂)
Тогда решение: {-8-4 ; 5-2} = {-12;3}
2) Воспользуемся формулой нахождения длины вектора: вектор |OP| (то есть серединная прямая АВ) = √x²+y²
Тогда решение: OP = √(-8²)+5² = 64+25 = 89
3) Воспользуемся формулой нахождения координат середины отрезка: x = 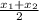 ; y =
; y = 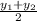
Тогда: x = 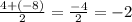 ; y =
; y = 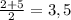
4) Строим центр окружности на координатных прямых, радиус окружности которой равняется 4. Нам нужно уравнение окружности. (Сорян, построишь сам всё, села батарея на телефоне)
Формула уравнения: (x - a)² + (y - b)² = r², а известные нам значения: a = 5, b = -6, r = 4
Вставляем в уравнение и решаем:
(x-5)² + (y+6)² = 16, распишем.
x²-10x+25 + y²+12y+36 = 16
x²-10x+25 + y²+12y+20 = 0
Решаем дискриминанты:
1) x²-10x+25 = 0
D = b²-4ac => (-10²)-4*1*25 = 100-100 = 0=0, 1 корень.
x = 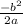
x₁ = 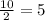
2) y²+12y+20 = 0
D = b²-4ac => 12²-4*1*20 = 144 - 80 = √64 = 8>0, 2 корня.
x = 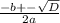
x₁ = 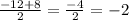
x₂ = 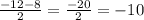
ответ: -10; -2; 5.
Пошаговое объяснение:
Наименьшее общее кратное (НОК) двух целых чисел m и n- это наименьшее натуральное число, которе делится m и n без остатка
НОК (14, 28) = 28 (28 /14 =2; 28/28 =1)
НОК (8, 9) = 72 (72/8 = 9; 72 / 9 = 8)
7. Наибольшим общим делителем (НОД) для двух целых чисел. и. называется наибольший из их общих делителей.
Взаимно простые числа — целые числа, не имеющие никаких общих делителей, кроме ±1.
НОД (728, 1275) = 1
НОК (728, 1275) = 928200, т. е. (728 * 1275) - взаимно простые числа
НОД (12,18) = 6 (т.е. и число 12, и число 18 делятся на 6) - это не взаимно простые числа, т.к , кроме единицы, у них есть общий делитель 6.
2) неверно
3) верно (но не уверена)
4) верно (но не уверена)