Высота должна быть равна ![2\sqrt[3]{2}](/tpl/images/4978/9339/13558.png)
Пошаговое объяснение:
Пусть сторона основания равна x, тогда площадь основания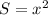 
.
Так как объем такой прямой призмы вычисляется по формуле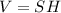 
, то
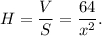
Площадь поверхности без крышки состоит из четырех площадей одинаковых боковых граней, каждая из которых прямоугольник со сторонами 
и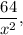 
и площади основания (дна), поэтому она равна
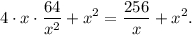
Найдем минимум функции
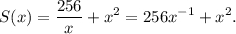
Вычислим производную, применяя формулу ![\[({x^n})' = n{x^{n - 1}},\]](/tpl/images/4978/9339/a792e.png)
и приравняем ее нулю.
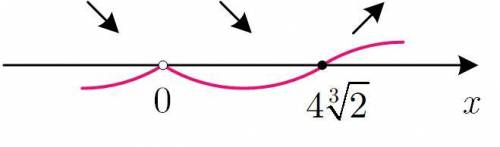
![S'(x) = - \displaystyle\frac{{256}}{{{x^2}}} + 2x = 0;displaystyle\frac{{2{x^3} - 256}}{{{x^2}}} = 0;2{x^3} = 256;{x^3} = 128;x = \sqrt[3]{{{2^7}}} = 4\sqrt[3]{2}.](/tpl/images/4978/9339/8a38b.png)
С метода интервалов убеждаемся, что проходя через эту точку производная меняет свой знак с минуса на плюс, таким образом, в этой точке достигается минимум функции.
При найденном значении высота равна
![H = \displaystyle\frac{{64}}{{{x^2}}}=\displaystyle\frac{{64}}{{{16\sqrt[3]{4=2\sqrt[3]{2}.](/tpl/images/4978/9339/d75a4.png)
Последняя цифра произведения равна 4, её мы получаем при умножении z на z. Если одноцифровое число при умножении само на себя даёт последнюю цифру 4, то это может быть либо 2, либо 8: 2*2=4, 8*8=64, другие произведения одинаковых чисел на самих себя не дадут в последнем разряде 4.
Предположим, что z=8. Исходя из вариантов ответа, сумма x+y+z теперь может быть либо 8, либо 9, так как z=8, а меньше чем 8 уже нельзя получить.
Если сумма цифр равна 8, то тогда х+у=0, значит, и х, и у равны 0. Но х стоит в начале первого числа, значит, он не может быть равен 0.
Если же сумма цифр равна 9, то тогда единственный подходящий вариант, когда х=1 и у=0.
Подставим х=1, у=0, z=8 в левую часть уравнения:
Первое число: 18
Второе число: 408
18×408 действительно получается 7344
ответ: А) 9
