4x3 в тетради начерти и 1см отрезок
190 прямых
Пошаговое объяснение:
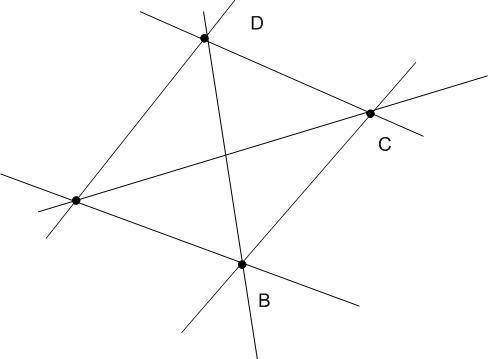
попробуем построить, ну, например для 4-х точек (см.рис).
Прямая проходит через каждые две точки. Т.е. нужно посчитать сколько различных пар точек можно выбрать из 4-х точек. Это - известная в комбинаторике формула для подсчета числа сочетаний (именно сочетаний, а не размещений, потому, что прямая АВ и прямая ВА - одна и таже прямая). Подсчитаем для 4-х точек:
C₄²=4!/(4-2)!4!=4!/(2!*2!)=3*4/2=6;
и действительно видим 6 прямых. Тогда для 20 точек:
C₂₀²=20!/((20-2)!2!)=19*20/2=190.
1) 12x = 60 х= 5
2) 33y = 132 у= 4
3) 512 = 357 где неизвестное??
4) 2x – 15 = 13 х= 14
5) 7y - 25 = 45 у=10
6) 130 - 4x = 70 - 4х= 70-130 -4х=-60 х= 15
7) 49 - 3x = 34 -3х=-15 х=5
8) 9y - 89 = 55 9у= 144 у=16
9) 74 - 82 = 2
Пошаговое объяснение:
Пошаговое объяснение:
1) х + 23 = 41
х=41-23
х= 18
2) 36 + y = 74
у=74-36
у= 38
3) 85 + z = 97
z=97-85
z= 12
4) x - 61 = 17
x=61+17
x=77
5) 46 - y = 24
y=46-24
y=22
6) 53 - z = 25
z= 53-25
z=28
7) m : 21 = 10
m=21*10
m=210
8) 192: n = 16
n=192:16
n=12
9) k : 44 = 20
k=20*44
k=880
105.
1) 12x = 60
x=60:12
x=5
2) 33y = 132
y=132:33
y=4
3) 51z = 357
z=357:51
z=7
4) 2x - 15 = 13
2х=15+13
2х=28
х= 28:2
х=14
5) 7y - 25 = 45
7y=45+25
7y=70
y=70:7
y=10
6) 130-4x = 70
4x=130-70
4x=60
x=60:4
x=15
7) 49 - 3x = 34
3x=49-34
3x=15
x=15:3
x=5
8) 9y – 89 = 55
9y=55+89
9y=144
y=144:9
y=16
9) 74 - 8z = 2.
8z=74-2
8z=72
z=72:8
z=9
можно начертить квадрат площадь которого равна 9см