Пошаговое объяснение:
есть чудесный метод , называется метод неопределенных коэффициентов
но мне лень и я решил те же коэффициенты подсчитать по другому
5/((x-2)(x+4)(x+6)) = A/(x-2)+B/(x+4)+C/(x+6)
поднимите руку кому не лениво вычислять А В С в лоб.
вижу что негусто, поэтому схитрю
при х->2 выражение сильно стремится к бесконечности и ведет себя как
5/((x-2)(x+4)(x+6)) = 5/((x-2)(2+4)(2+6))=5/48 * 1/(x-2)
Вы заметили что мы только что вычислили А ???
при х->-4 выражение сильно стремится к бесконечности и ведет себя как
5/((x-2)(x+4)(x+6)) = 5/((-4-2)(х+4)(-4+6))=-5/12 * 1/(х+4)
при х->-6 выражение сильно стремится к бесконечности и ведет себя как
5/((x-2)(x+4)(x+6)) = 5/((-6-2)(-6+4)(x+6))=5/16 * 1/(x+6)
конечный оtвет
5/48*ln(|x-2|) - 5/12*ln(|х+4|) + 5/16 *ln(|x+6|) + const
Пошаговое объяснение:
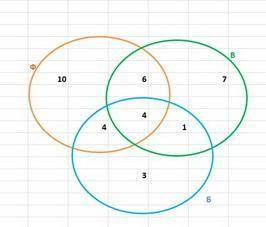
задача решается при кругов Эйлера
у нас
всего 35
ф =24
в = 18
б =12
ф+в =10
ф+б = 8
в+б =5
будем смотреть на круги и считать
если мы сложим ф+в просто как 24+18 то увидим, что те, кто занимается двумя этими видами одновременно, учтутся 2 раза. поэтому правильное объединение множеств будет ф∪в = 24+18-10
если мы сюда добавим баскетбол просто как 12, то увидим, что дважды учтутся те, кто занимается ф+б и в+б. поэтому их надо тоже вычесть
т.о. получится такое объединение множеств ф∪в∪б = 24+18-10+12-8-5
но при этом те, кто занимается сразу всеми видами отнялись дважды.
поэтому их надо прибавить еще раз. их у нас Х.
вот, получили формулу
ф∪в∪б = 24+18-10+12-8-5+ Х =35
31+Х=35
Х=4
теперь заполним круги и проверим весь счет
Ф =10+6+4+4=24
в = 7+6+4+1=18
б = 4+4+1+3=12
ф+в 6+4=10
в+б = 4+1=5
ф+б = 4+4 = 8
10+6+7+4+4+1+3=35
круги Эйлера построены верно, задача решена верно - сразу тремя видами спорта занимаются 4 ученика
Дежурят - сказуемое