ответ: 180.
Вот формула площади трапеции:
, где a и b - основания трапеции, а h - высота (S, разумеется, площадь).
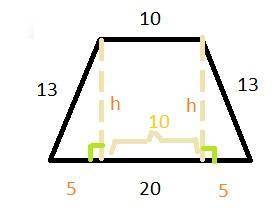
Вот только одна проблема: мы не знаем высоты. Но чтобы ее узнать, можно отсечь от трапеции (например, справа) прямоугольный треугольник. Его гипотенуза (c)- это боковая сторона трапеции, которая равна 13. Нижний катет (b) будет равен 
. Почему - можно увидеть на рисунке ниже. Второй катет этого треугольника (а) - это и есть высота, которую можно найти по теореме Пифагора:
Теперь высоту мы знаем и можем найти площадь трапеции:
Задача решена!
Пример:
известны координаты 25 точек:
A(7 ; 18) , B(9 ; 18) , C(14 ; 22) , D(14 ; 24) , E(18 ; 19) , F(17 ; 15) , G(20 ; 10) , H(17 ; 3) , I(19 ; 1) , J(15 ; 1) , K(14 ; 3) , L(11 ; 3) ,
M(12 ; 1) , N(7 ; 1) , O(2 ; 11) , P(1 ; 18) , Q(2 ; 23) , R(5 ; 24) , S(7 ; 22) , T(5 ; 11) , U(8 ; 7) , V(12 ; 7) , W(16 ; 11) , X(16 ; 14) , Y(11 ; 14) .
Если отметить эти точки на координатной плоскости, а затем соединить их отрезками в последовательности A — B — C — D — E — F — G — H — I — J — K — L — M — N — O — P — Q — R — S — T — U — V — W — X — Y — A , то получим рисунок.
Пошаговое объяснение что по частям
