Обозначим данный ромб буквами ABCD.
AC и BD - диагонали ромба ABCD.
Е - точка пересечения диагоналей AC и BD.
AC = 30 дм.
BD = 40 дм.
Ромб - параллелограмм, у которого все стороны равны.
⇒ AB = BC = CD = AD.
Т.к. ромб - параллелограмм ⇒ диагонали ромба точкой пересечения делятся пополам (свойство параллелограмма).
⇒ АЕ = ЕС = AC/2 = 30/2 = 15 дм
⇒ DE = EB = DB/2 = 40/2 = 20 дм.
Диагонали ромба взаимно перпендикулярны.
⇒ ΔАЕВ - прямоугольный.
Найдём сторону ромба АВ, по теореме Пифагора: (с² = а² + b², где с - гипотенуза; а, b - катеты).
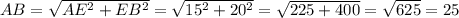 дм.
дм.
ответ: 25 дм.
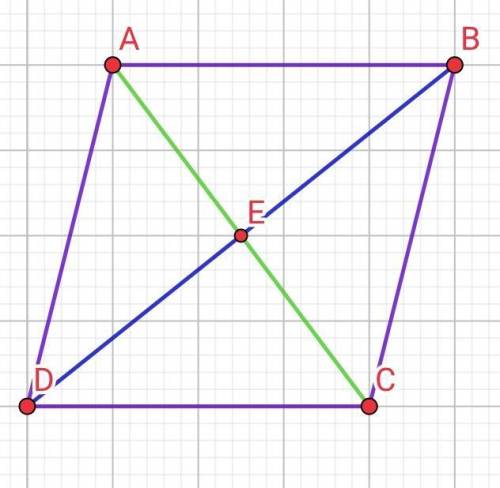
8,5-6,5+x=3,8
x=3,8-8,5+6,5
x=1,8
(х+12/13)- 1 11/13=1 1/13
x+12/13=1 1/13+1 11/13
x+12/13=2 12/13
x=2 12/13-12/13
x=2
14/15-(2/3-х)=1,8
14/15-2/3+x=18/10
x=18/10-14/15+2/3
x=(54-28+20)/30
x=46/30=1 16/30=1 8/15
-(9,8-х)-10,5=-20,8
-9,8+x-10,5=-20,8
x=-20,8+9,8+10,5
x=-0,5
Вычислите значения выражений,раскрыв скобки:
1)(20-(-6))-(15-(-12))=20+6-15-12=-1
2)-29-(18-74)-(74-19)=-29-18+74-74+19=-28
3)-(-65)-(-55-39)-(-34)=65+55+39+34=193
4)-48-(-22)-(-34-(-3))=-48+22+34-3=5