Мамонты стали вымирать ещё в давние времена,около 11 тыс.лет тому назад.Причиной вымирания стало потепление климата.Это были крупные животные.которые передвигались небольшими группами и питались травой,листвой деревьев и кустарников.Продолжительность жизни составляла в среднем 50 лет,отдельные особи доживали и до 80 лет.Вес составлял около 100 кг,а тело было покрыто шерстью. Мамонты при жить в районах лесостепи и тундры.Поэтому их останки часто находили именно в этих районах. В 18-19 вв. находили останки мамонтов в р-не Сибири,около 20 находок.Они хорошо сохранились,скелеты имели остатки кожи и ткани.В 20 в.находки участились.Памятником природы считается "кладбище"мамонтов в р-не реки Берелех в Якутии. Самые известные находки: Березовский мамонт 1900г. Магаданский мамонтёнок Дима 1977г. Ямальский мамонтёнок 1988 г. Ленский мамонт 1806 г. Таймырский мамонт 1948 г.
Мамонты стали вымирать ещё в давние времена,около 11 тыс.лет тому назад.Причиной вымирания стало потепление климата.Это были крупные животные.которые передвигались небольшими группами и питались травой,листвой деревьев и кустарников.Продолжительность жизни составляла в среднем 50 лет,отдельные особи доживали и до 80 лет.Вес составлял около 100 кг,а тело было покрыто шерстью. Мамонты при жить в районах лесостепи и тундры.Поэтому их останки часто находили именно в этих районах. В 18-19 вв. находили останки мамонтов в р-не Сибири,около 20 находок.Они хорошо сохранились,скелеты имели остатки кожи и ткани.В 20 в.находки участились.Памятником природы считается "кладбище"мамонтов в р-не реки Берелех в Якутии. Самые известные находки: Березовский мамонт 1900г. Магаданский мамонтёнок Дима 1977г. Ямальский мамонтёнок 1988 г. Ленский мамонт 1806 г. Таймырский мамонт 1948 г.
Даны 2 функции: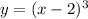 и
и 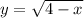 .
.
первая - кубическая парабола, сдвинутая на 2 единицы в область положительных значений аргумента, функция возрастает,
вторая - ветвь параболы по оси Ох, функция убывает.
Это означает, что графики этих функций пересекаются внутри заданной области, фигура состоит из двух частей.
Находим крайние точки фигуры как точки пересечения с осью Ох при у = 0.
Правая точка. √(4 - x) = 0, возводим в квадрат обе части: х = 4.
Левая точка. (x - 2)^3 = 0, извлекаем кубический корень из обеих частей: х = 2.
Теперь находим точку пересечения: (x - 2)^3 = √(4 - x). Отсюда видно, что корень равен х = 3.
Теперь можно определить искомую площадь как сумму двух интегралов: