1) Строим отрезок, равный радиусу. Например, 2 см. То есть r = 2 см.
2) Отмечаем центр окружности (им будет край отрезка).
3) Измеряем циркулем отрезок, проводим окружность. Раствор циркуля должен оставаться неизменным.
4) Прикладываем линейку к радиусу и "продлеваем" его до пересечения с окружностью.
5) Чтобы узнать длину радиуса, нужно измерить расстояние от центра окружности до любой точки окружности.
упрощённый)
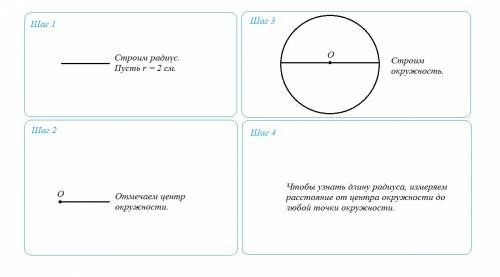
1) Берем произвольную длину радиуса. Пусть r = 2 см.
2) Так как радиус равен половине диаметра, то получаем следующее (вместо r подставляем значение радиуса):
d = 2r ⇒
d = 2·2 = 4 (см) - длина диаметра.
3) Отмечаем центр отрезка (диаметра). Это будет центр окружности.
Пусть O – центр окружности.
4) Строим окружность с центром в точке О.
5) Чтобы узнать длину радиуса, измеряем расстояние от центра окружности до любой точки окружности.
Площадь квадрата находят по формуле S = a², где а - сторона квадрата, S - его площадь.
Площадь прямоугольника находят по формуле S = a · b, где S - площадь, a и b - его стороны (длина и ширина).
Периметр прямоугольника находят по формуле Р = 2(а + b), где Р - периметр, а и b - стороны (длина и ширина).
Найдем площадь квадрата: S = (5/9)² = 5/9 · 5/9 = 25/81 (дм²).
Т.к. площадь квадрата равна площади прямоугольника и ширина прямоугольника равна 2 целых 1/2, то его длина равна:
25/81 : (2 целые 1/2) = 25/81 : 5/2 = 25/81 · 2/5 = 10/81 (дм).
Тогда периметр прямоугольника равен:
Р = (10/81 +2 целые 1/2) · 2= (20/162 + 2 целые 81/162) · 2 =
= (2 целые 101/162) · 2 = 425/162 · 2 = 425/81 = 5 целых 20/81 (дм).
ответ: 5 целых 20/81 дм.