Чтобы найти сколькими нулями оканчивается произведение нужно найти сколько раз в этом произведении встречается множитель 10.
Заметим, что 10 раскладывается на простые множители как 10=2·5. Очевидно, сомножителей "2" будет больше чем сомножителей "5". Таким образом, нужно узнать число множителей "5" в произведении. Каждый такой множитель в паре с множителем "2" даст множитель "10" и соответственно дополнительный ноль на конце числа.
Найдем, сколько чисел содержит множитель "5". Всего среди первых 2020 натуральных чисел таких чисел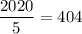 
, но в данном произведении отсутствуют первых три числа кратные 5 (5, 10, 15). Значит, множитель "5" содержит 404-3=401 число.
Но некоторые числа содержат не один множитель "5", а два. Найдем количество таких чисел.
Для этого разделим 2020 на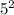 
:
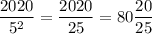
Значит, последнее число, которое содержит в своем составе два множителя "5" - это число 
. Первое такое число - очевидно, 25. Значит, всего таких чисел 80.
Еще некоторые числа содержат три множителя "5". Найдем количество таких чисел. Для этого разделим 2020 на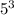 
:
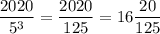
Значит, последнее число, которое содержит в своем составе три множителя "5" - это число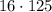 
. Первое такое число - 125. Значит, всего таких чисел 16.
И, наконец, некоторые числа содержат сразу четыре множителя "5". Найдем их количество. Для этого разделим 2020 на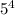 
:
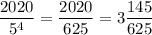
Значит, последнее число, которое содержит в своем составе четыре множителя "5" - это число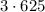 
. Первое такое число - 625. Значит, всего таких чисел 3.
Чисел, кратных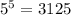 
среди множителей нет.
Итак, 401 число содержат в своем составе множитель "5", 80 чисел содержат второй множитель "5", 16 чисел содержит третий множитель "5" и 3 числа содержат четвертый множитель "5". Значит, всего множителей "5" имеется:
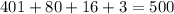
Значит, число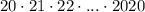 
оканчивается 500 нулями.
ответ: 500
Пошаговое объяснение:
6x²-7x+1<0
Допустим:
6x²-7x+1=0; D=49-24=25
x₁=(7-5)/12=2/12=1/6
x₂=(7+5)/12=12/12=1
- + -
.·.
1/6 1
x∈(1/6; 1)
5x²-4x-1>0
Допустим:
5x²-4x-1=0; D=16+20=36
x₁=(4-6)/10=-2/10=-0,2
x₂=(4+6)/10=10/10=1
+ - +
..
-0,2 1
x∈(-∞; -0,2)∪(1; +∞)
x²+8x<0
Допустим: x²+8x=0
x(x+8)=0; x₁=0
x+8=0; x₂=-8
- + -
..
-8 0
x∈(-8; 0)
8x²+10x-3≥0
Допустим:
8x²+10x-3=0; D=100+96=196
x₁=(-10-14)/16=-24/16=-3/2=-1,5
x₂=(-10+14)/16=4/16=1/4=0,25
+ - +
..
-1,5 0,25
x∈(-∞; -1,5]∪[0,25; +∞)
2y²+9y+9≤0
Допустим:
2y²+9y+9=0; D=81-72=9
y₁=(-9-3)/4=-12/4=-3
y₂=(-9+3)/4=-6/4=-3/2=-1,5
- + -
..
-3 -1,5
y∈[-3; -1,5]
x²+7x-60<0
Допустим:
x²+7x-60=0; D=49+240=289
x₁=(-7-17)/2=-24/2=-12
x₂=(-7+17)/2=10/2=5
- + -
..
-12 5
x∈(-12; 5)
x²<4
Допустим:
x²=4; x=±√4=±2
- + -
..
-2 2
x∈(-2; 2)
(2(x-5))²<1
(2x-10)²<1
4x²-40x+100<1
4x²-40x+100-1<0
4x²-40x+99<0
Допустим:
4x²-40x+99=0; D=1600-1584=16
x₁=(40-4)/8=36/8=9/2=4,5
x₂=(40+4)/8=44/8=11/2=5,5
- + -
..
4,5 5,5
x∈(4,5; 5,5)
30+15=45 ц на машине с прицепом
1080:45 = 24 рейса надо сделать