Чему равна площадь комнаты, имеющей форму прямоугольника с размерами 5 и =

👇

Увидеть ответ

Ответ:

Kristinapermya

19.08.2022

$5 \frac{1}{2} *3 \frac{1}{2}= \frac{11*7}{2*2} = \frac{77}{4} =19 \frac{1}{4}$

4,7(26 оценок)

Открыть все ответы

Ответ:

syrlybai056

19.08.2022

Это пойдёт?

Моя семья в годы Великой Отечественной Войны.

Почти 70 лет со времени окончания Великой Отечественной Войны. Страшное было время. Много людей погибло на той войне. Это были не только солдаты, воевавшие на фронте, но и мирные люди: старики, женщины, дети, которые оказались на земле, захваченной врагом. В глубоком тылу, вдалеке от войны, люди, борясь с голодом и холодом, делали всё фронта, всё для Победы! Колхозники растили хлеб, заготавливали мясо, молоко, табак. Рабочие на заводах и фабриках без выходных и отпусков делали патроны, снаряды, винтовки, танки, самолёты; шили форму и шинели, точали сапоги для солдат, а чтобы красноармейцы не мёрзли в зимнюю стужу, шили тёплые полушубки и катали валенки. А самое главное, ежедневно, с надеждой слушали военные известия с фронтов, ждали редкие письма от своих родных отцов, братьев, сыновей, воевавших в окопах Великой войны. Страшно было получить "похоронку" - официальное извещение о гибели солдата. А ещё страшнее было узнать о том, что он "пропал без вести" или попал в плен к врагам. В то суровое время это считалось изменой Родине.

4,4(4 оценок)

Ответ:

эмилисенок2

19.08.2022

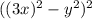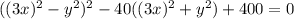Для начала поработаем со вторым выражением. Первые три слагаемых свернем в квадрат разности: $((3x)^{2}-y^{2})^{2}$ ; В следующих двух слагаемых вынесем общий множитель "40": $40(9x^{2}+y^{2})=40((3x)^{2}+y^{2})$ ; В итоге получим следующее уравнение: $((3x)^{2}-y^{2})^{2}-40((3x)^{2}+y^{2})+400=0$ . В скобках мы видим похожие выражения, отличающиеся лишь знаком посередине (такие выражение называются сопряженными). А хотелось бы видеть там равные (строго говоря тождественные) выражения. 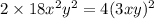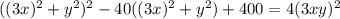Пусть в первой скобке вместо $(3x)^{2}-y^{2}$ будет стоять $(3x)^{2}+y^{2}$ ; Это приведет к тому, что придется убавить $2\times 18x^2y^2=4(3xy)^{2}$ ; В итоге: $((3x)^{2}+y^{2})^{2}-40((3x)^{2}+y^{2})+400= 4(3xy)^{2}$ ; Слева стоит квадрат суммы. 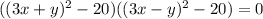Уравнение примет вид: $((3x)^{2}+y^{2}-20)^{2}=(6xy)^{2} \Leftrightarrow ((3x)^{2}+y^{2}-20+6xy)((3x)^{2}+y^{2}-20-6xy)=0$ ; Сворачивая еще раз: $((3x+y)^{2}-20)((3x-y)^{2}-20)=0$ ; Получаем серию прямых: $\pm 3x+\sqrt{20},\; \pm3x-\sqrt{20}$ ; А теперь приступим к рассмотрению первого уравнения.

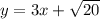Это уравнение задает круг с центром в точке (0, 0) и радиусом $\sqrt{2}$ ; Рассмотрим прямую $y=3x+\sqrt{20}$ ; Найдем радиус окружности с центром в начале координат, которая касается данной прямой. Это легко сделать из подобия треугольников. 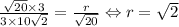$\frac{\sqrt{20}\times 3}{3\times 10\sqrt{2}}=\frac{r}{\sqrt{20}} \Leftrightarrow r=\sqrt{2}$ ; Значит, круг касается всех этих четырех прямых. Достаточно найти только координаты касания с любой из прямых. Это делается так же, как и находился радиус окружности. Для той же прямой это координаты 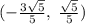$(-\frac{3\sqrt{5}}{5},\; \frac{\sqrt{5}}{5} } )$ ; Ну а все решения:

$(\frac{3\sqrt{5}}{5},\; \frac{\sqrt{5}}{5}),\; (\frac{3\sqrt{5}}{5},\; -\frac{\sqrt{5}}{5}),\; (-\frac{3\sqrt{5}}{5},\; \frac{\sqrt{5}}{5}),\; (-\frac{3\sqrt{5}}{5},\; -\frac{\sqrt{5}}{5})$