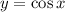
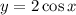
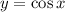 . Отличается лишь область значений.
. Отличается лишь область значений.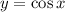 область значений следующая:
область значений следующая:![E(\cos x)=[-1,1]](/tpl/images/0579/2389/1dd9b.png)

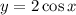 :
: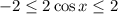
![E(y)=[-2,2]](/tpl/images/0579/2389/4690c.png)
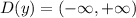 - область определения
- область определения 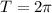 - период функции (все тригонометрические функции периодичны) .
- период функции (все тригонометрические функции периодичны) .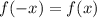
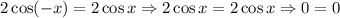 - тождество.
- тождество.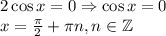
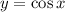 достигает экстремумы на концах отрезка области значения, то и
достигает экстремумы на концах отрезка области значения, то и 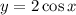 достигает экстремумы на концах отрезка:
достигает экстремумы на концах отрезка:![[-2,2]](/tpl/images/0579/2389/82b6c.png)
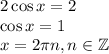 - максимумы.
- максимумы.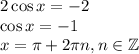 - минимумы.
- минимумы. и на интервалах, получаемые сдвигом этого интервала на
и на интервалах, получаемые сдвигом этого интервала на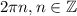
 и на интервалах, получаемые сдвигом этого интервала на
и на интервалах, получаемые сдвигом этого интервала на 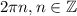
![[\pi,2\pi]](/tpl/images/0579/2389/a222e.png) и на отрезках, получаемых сдвигами этого отрезка на
и на отрезках, получаемых сдвигами этого отрезка на 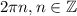
![[0,\pi]](/tpl/images/0579/2389/2a07b.png) и на отрезках, получаемых сдвигами этого отрезка на
и на отрезках, получаемых сдвигами этого отрезка на 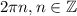

1) Если перед скобками стоит знак "+" или знака нет, то скобки можно просто опустить, сохранив при этом знаки слагаемых, стоящих в этих скобках.
Например:
2) Если перед скобками стоит знак "-", то чтобы раскрыть скобки, необходимо сначала поменяв знаки всех слагаемых в скобках
на противоположные, затем сменить знак перед скобками на "+" и после этого можно просто опустить скобки.
(или при раскрытии скобок умножать каждое слагаемое на "-1")
Пример: