681077
Пошаговое объяснение:
Нужно вычислить сумму
S=1+4+7++2017+2020.
Каждое слагаемое отличается на 3 от предыдущего слагаемого, то определим количество слагаемых в сумме по правилу счёта
(2020-1):3+1=2019:3+1=673+1=674.
Перепишем сумму в двух видах:
S= 1 + 4 + 7 ++2014+2017+2020
S=2020+2017+2014+... + 7 + 4 + 1
И сложим почленно:
2 · S= (1+2020) + (4+2017) + (7+2014)++(2014+7)+(2017+4)+(2020+1)=
=2021+2021+2021+...+2021+2021+2021=674·2021.
Тогда
S=674·2021:2=337·2021=681077.
Рассмотрим сумму как сумма n= 674 элементов арифметической прогрессии с a₁=1, a₆₇₄=2020. Тогда
S₆₇₄=(a₁+a₆₇₄)·674:2=(1+2020)·337=2021·337=681077.
1 (-бесконечность;+бесконечность) 2 (- бесконечность;-7\4)U(-7\4;+бесконечность) 3 [-7;+бесконечность) 4 (-бесконечность;1/2) 5(-бесконечность;3)U(-3;0)U(0;3)U(3;+бесконечность) 6(-бесконечность;+бесконечность)
Пошаговое объяснение:
Область определения это такие числа, которые может принимать переменная x.
1. 
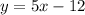(здесь при любых числах выражение решается,т.е. нет ограничений => (-бесконечность;+бесконечность)
2. 
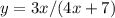(В данном случае, ограничение присутствует, знаменатель дроби не должен быть равен нулю. (старое правило-на 0 делить нельзя)
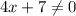
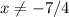=> (- бесконечность;-7\4)U(-7\4;+бесконечность)
3.
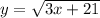(Под корнем всегда должно быть неотрицательное число)
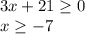[-7;+бесконечность)
4.
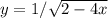(знаменатель не должен быть равен 0, а так же не должен быть отрицательным)
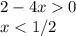(-бесконечность;1/2)
5. 
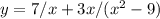(знаменатель не должен быть равен 0)
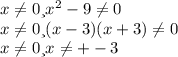(-бесконечность;3)U(-3;0)U(0;3)U(3;+бесконечность)
6.
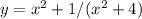(знаменатель не должен быть равен 0, но если решить, можно понять что знаменатель положителен при любых x)
(-бесконечность;+бесконечность)
