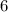 раз больше, поскольку мы различаем
раз больше, поскольку мы различаем 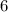 комбинаций ABC, ACB, BAC, BCA, CAB и CBA. Поэтому для получения конечного числа комбинаций нужно промежуточный вариант разделить на
комбинаций ABC, ACB, BAC, BCA, CAB и CBA. Поэтому для получения конечного числа комбинаций нужно промежуточный вариант разделить на 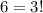
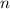 условно-различимых объектов нужно делить промежуточное число на
условно-различимых объектов нужно делить промежуточное число на 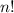
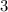 яблока
яблока 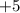 груш
груш 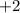 персика
персика  апельсин
апельсин 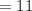 объектов.
объектов.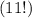
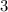 яблока, а значит
яблока, а значит 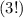 всех перестановок не различимы и нужно разделить на
всех перестановок не различимы и нужно разделить на 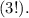
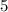 груш, а значит
груш, а значит 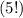 всех перестановок не различимы и нужно разделить на
всех перестановок не различимы и нужно разделить на 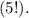
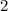 персика, а значит
персика, а значит 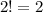 всех перестановок не различимы и нужно разделить на
всех перестановок не различимы и нужно разделить на 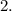
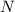 равно:
равно: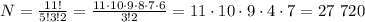
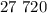 вариантов.
вариантов.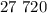 теоретически, конечно, можно было бы выписать, чтобы проиллюстрировать всю картину вариантов, но это заняло бы очень большой объём трудно воспринимаемого текста, поэтому, если уж и попытаться перечислить все возможные варианты, то тогда лучше составить полностью аналогичную модель на меньших числах. Возьмём не
теоретически, конечно, можно было бы выписать, чтобы проиллюстрировать всю картину вариантов, но это заняло бы очень большой объём трудно воспринимаемого текста, поэтому, если уж и попытаться перечислить все возможные варианты, то тогда лучше составить полностью аналогичную модель на меньших числах. Возьмём не 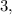 а
а 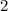 яблока, не
яблока, не 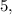 а
а 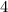 груши, избавимся от персиков и оставим апельсин.
груши, избавимся от персиков и оставим апельсин.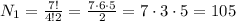 ;
;