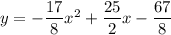
Пошаговое объяснение:
Уравнение параболы в общем виде записывается следующим образом:
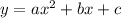
где 
, 
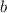и 
-- коэффициенты, которые нам необходимо найти.
Подставим известные нам точки в уравнение параболы и составим систему из трёх уравнений:
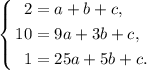
Эту систему можно решать по-разному, дело вкуса. Даю простейшее решение с выражением каждого неизвестного по-очереди.
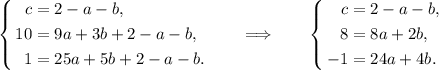
Умножим второе уравнение на 2 и вычтем из третьего второе, чтобы избавиться от :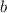
Отсюда видно, что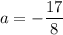 
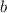, получаем из второго уравнения, а из первого:
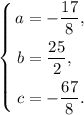
Таким образом, 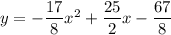- уравнение нашей параболы.
b=7
a=3.5.тогда 1.2*(7*3.5)=12.25