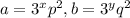 , где p и q - натуральные числа, не делящиеся на 3. Ясно, что x<n, y<n. Если x=y, то, разделив обе части на
, где p и q - натуральные числа, не делящиеся на 3. Ясно, что x<n, y<n. Если x=y, то, разделив обе части на 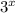 , получим уравнение
, получим уравнение 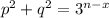 . Поскольку числа p и q не делятся на 3, а величина n-x больше 0, это уравнение корней не имеет. Наконец, рассмотрим случай, когда x≠y, в силу симметрии можно считать, что x<y. Разделив уравнение на
. Поскольку числа p и q не делятся на 3, а величина n-x больше 0, это уравнение корней не имеет. Наконец, рассмотрим случай, когда x≠y, в силу симметрии можно считать, что x<y. Разделив уравнение на 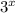 , имеем
, имеем 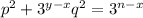 . Первое слагаемое не делится на 3, второе и третье делятся, получили противоречие.
. Первое слагаемое не делится на 3, второе и третье делятся, получили противоречие.
2. Если ученик опоздал на урок, то учитель весь день не спрашивает у него домашнее задание.
3. Надо обязательно поболтать с подругой(другом) на уроке.
4. Если учитель увидел у ученика шпаргалку, то учитель даже не будет проверять эту работу(для которой написана шпаргалка), а сразу поставит оценку 4.
5. Хотя бы раз в две недели ученик обязан сбить на своем пути младшеклашку.
6. Если за контрольную ни один ученик не получил 2, то следующий день - выходной(на следующий день не надо идти в школу).