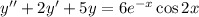
Общее решение неоднородного дифференциального уравнения равно сумме общего решения однородного дифференциального уравнения, соответствующего данному неоднородному, и частного решения неоднородного дифференциального уравнения.
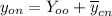
Составим однородное дифференциальное уравнение, соответствующее данному неоднородному:
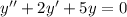
Составим характеристическое уравнение и решим его:
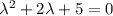
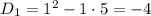
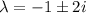
Общее решение однородного уравнения:
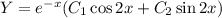
Запишем в общем виде частное решение данного неоднородного уравнения, учитывая, что в правой части стоит произведение экспоненты и на косинус, а также то, что степень экспоненты и выражение под знаком косинуса совпадают с соответствующими выражениями, полученными при решении однородного уравнения:
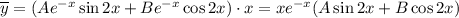
Находим первую производную:
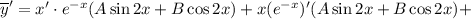
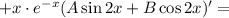
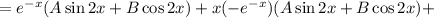
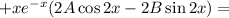
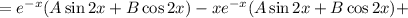
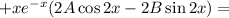
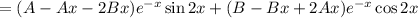
Находим вторую производную:
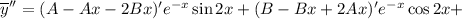
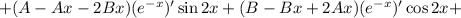
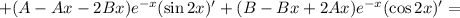
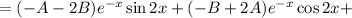

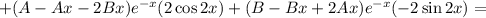
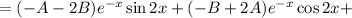
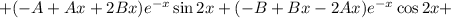
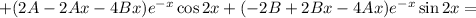
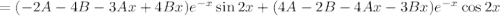
Подставляем в исходное уравнение:
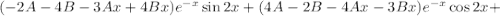
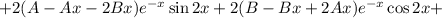
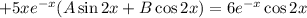
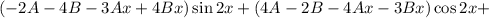
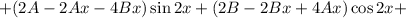
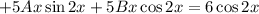
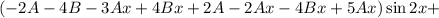
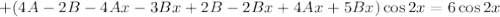
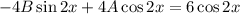
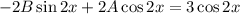
Условие равенства левой и правой частей:
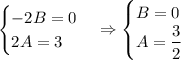
Частное решение данного неоднородного уравнения:
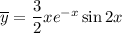
Общее решение данного неоднородного уравнения:
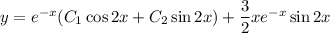
в) -0,7∙3,2=-2,24
б) -12∙(-13) = 146
2. Выполните деление:а) -69:23=-3
в) 0,84:(-2,4)=-0,5
б) -35:(-7)=5
3. Решите уравнения)
-1,4х =-4,27
х=-4,27:(-1,4)
х=3,05
б) у:3,1 = -6,2
у=-6,2*3,1
у= -19,22
4 Представьте числа и в виде периодических дробей. Запишите приближенные значения данных чисел, округлив периодические дроби до сотых. нет самих чисел
5. Сколько целых решений имеет неравенство |y|<72?
от -71 до 71, т.е. 71 (отрицательных) +71 (положительных)+1 (ноль)=143