Олимпийское движение постоянно совершенствуется, со временем
приобретая положительные тенденции своего развития. МОК (Международный
Олимпийский комитет) уделяет немало внимания проблемам Игр и по мере сил
старается их решить. Это, в частности, касается организации Юношеских
Олимпийских игр. Первые летние Игры начали проводить только с 2010 года, а
зимние – с 2012. Предшественниками юношеской Олимпиады стали всемирные
соревнования, в которых принимали участие спортсмены-юниоры, возраст
которых варьировал от 14 до 18 лет. Целью организации подобных
мероприятий стало стремление вовлечь молодежь в официальное Олимпийское
движение юниорам реализовать таланты, а также найти сильных
спортсменов, которые будут достойны представлять свои страны на
последующих Играх.
Прекрасным примером достойного участника юношеской Олимпиады
является Никита Владимирович Нагорный, российский гимнаст, рожденный 12 февраля 1997 года в Ростове-на-Дону. Никита в свои девятнадцать является
трехкратным чемпионом, серебряным и бронзовым призѐром юношеских
Олимпийских игр 2014 года, чемпионом Европы 2015 года в опорном прыжке,
чемпионом Европы 2016 в командном первенстве и в вольных упражнениях,
серебряным призѐром летних Олимпийских игр 2016 года. Он - заслуженный
мастер спорта России, а также мастер спорта международного класса, а ко
всему еще и младший лейтенант Вооруженных Сил Российской Федерации.
За высокие спортивные достижения, за волю к победе и
целеустремленность, Никите вручили медаль ордена «За заслуги перед Отечеством».
Другой положительной тенденцией развития Олимпийского движения в
лучшую сторону стало постепенное вовлечение в него женщин, а также
исправление гендерной асимметрии. Вплоть до 1981 года в МОК не входила ни
одна женщина, поскольку решение о составе Комитета принимали его
участники, т.е. мужчины.
Одним из примеров таких личностей является Ольга Геннадьевна
Вилухина, российская биатлонистка. Она занималась лыжными гонками до
1998 года, но с 2004 года перешла на биатлон по совету тренера. Чемпионат
мира по биатлону среди юниоров 2006 года стал для нее первым в карьере. В
индивидуальной гонке она заняла лишь 28 место.
На сегодняшний день Ольга является заслуженным мастером спорта
России, двукратным серебряным призером Олимпийских игр 2014 года (в
спринте и женской эстафете), бронзовым призером чемпионата мира 2012 года,
трехкратной чемпионкой России.
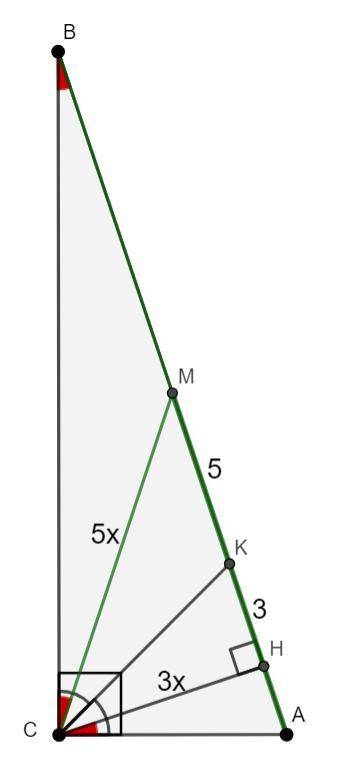
Поэтому K лежит на отрезке MH.
1.
Рассмотри ∠ACH и ∠ABC:
CA⊥BA и CH⊥BH по условию;
∠ACH = ∠ABC, как углы с взаимно перпендикулярными сторонами.
Медиана прямоугольного треугольника, проведённая к гипотенузе, равна половине гипотенузы.Поэтому CM = BM, тогда ΔBMC - равнобедренный.
Углы при основании равнобедренного треугольника равны.Поэтому ∠MBC = ∠MCB, откуда ∠ACH = ∠MCB (т.к. ∠ACH = ∠MBC).
∠ACK = ∠BCK, как углы при биссектрисе;
∠ACH = ∠MCB;
Тогда ∠ACK - ∠ACH = ∠BCK - ∠MCB;
∠HCK = ∠MCK.
Биссектриса треугольника делит сторону треугольника на отрезки, пропорциональные прилежащим сторонам.2.
Рассмотрим ΔMCH:
CK - биссектриса MCH, поскольку ∠HCK = ∠MCK;
Тогда справедливо равенство  ;
;
Пусть CM = 5x, тогда CH = 3x;
HM = HK+KM = 3+5 = 8;
ΔMCH - прямоугольный (CH⊥MH ⇒ ∠CHM = 90°);
Тогда по теореме Пифагора получим:
CH²+HM² = CM²;
(3x)²+8² = (5x)²;
9x²+64 = 25x²;
64 = 16x²;
x² = 64:16 = 2²;
x = 2.
CM = 5x = 5·2 = 10;
CH = 3x = 3·2 = 6.
3.
CM = BM = MA;
MA = 10;
AB = 2·MA = 2·10 = 20;
AH = MA-HM = 10-8 = 2.
4.
Рассмотрим ΔCHA:
∠CHA = 90°; AH = 2; CH = 6;
По теореме Пифагора найдём AC:
AC² = CH²+AH² = 6²+2² = 36+4 = 2²·10;
AC = 2√10.
5.
Рассмотрим ΔABC:
∠ACB = 90°; AC = 10√2; AB = 20;
По теореме Пифагора надём BC:
BC² = AB²-AC² = 20²-40 = 400-40 = 6²·10;
BC = 6√10.
6.
Рассмотрим ΔCHK:
∠CHK = 90°; CH = 6; HK = 3;
По теореме Пифагора найдём CK:
CK² = CH²+HK² = 6²+3² = 36+9 = 3²·5;
CK = 3√5.
ответ: AB = 20; BC = 6√10; AC = 2√10; CK = 3√5.