1.
Длина стороны квадрата равна см. Чему равны его периметр и площадь, если = 8?
Периметр квадрата равен сумме длин всех его сторон.
P = + + + или P = · 4
Площадь квадрата равна произведению длин двух его сторон.
S = ·
Периметр фигуры обозначают большой латинской буквой P, площадь — большой латинской буквой S, а стороны фигур — маленькими латинскими буквами , b и др.
Формулы — это равенства, которые устанавливают взаимосвязь между величинами.
2.
Составь формулу для вычисления периметра каждой фигуры. Между какими величинами они устанавливают взаимосвязь?
3.
Между какими величинами устанавливают взаимосвязь формулы:
S = c · c, P = c · 4?
4.
Составь формулы периметра и площади прямоугольника.
1) Длина прямоугольника равна см, ширина — b см. Чему равна его площадь, если = 11, b = 6?
2) Длина прямоугольника равна см, ширина — b см. Чему равен периметр, если = 12, b = 4?
Площадь прямоугольника равна произведению его длины и ширины.
S = · b, где S — площадь, — длина, b — ширина прямоугольника.
Периметр прямоугольника равен удвоенной сумме его длины и ширины.
P = ( + b) · 2, где P — периметр, — длина, b — ширина прямоугольника.
5.
Найди площадь и периметр прямоугольника со сторонами:
а) 9 см и 7 см;
б) 23 см и 4 см;
в) 18 см и 7 см;
г) 21 см и 3 см.
6.
Маша хочет обшить кружевом салфетку прямоугольной формы. Размеры салфетки 20 см и 25 см. Сколько сантиметров кружев ей потребуется? Укажи правильный ответ.
1) 45 см;
2) 95 см;
3) 90 см;
4) 85 см.
7.
1)Площадь прямоугольника 56 см2, ширина — 4 см. Чему равна длина прямоугольника?
2) Площадь прямоугольника ABCD равна 49 см2, а сторона AB равна 7 см. Найди длину стороны BC. Как называется прямоугольник ABCD?
Чтобы найти длину прямоугольника, надо его площадь разделить на ширину.
= S : b
8.
1)Запиши формулы периметра и площади квадрата со стороной b см.
2) Найди периметр и площадь квадрата, сторона которого равна 10 см.
3) Найди периметр квадрата, площадь которого 81 см2.
9.
Между какими величинами устанавливают связь формулы?
P = c · 6
S = c · c
S = c · b
P = c · 4
P = (c + b) · 2
P = c · 3
10.
Запиши формулы площади и периметра каждой фигуры, изображённой на рисунке.
Рассмотрим случай, при котором квадратный корень из числа не извлекается нацело, и необходимо найти её приближённое значение. Воспользуемся методом извлечение квадратных корней столбиком. Допустим, необходимо найти приближённое значение √7. Чтобы извлечь квадратный корень из 7, нужно:
Разбить число, из которого мы извлекаем квадратный корень, на разряды справа налево по 2 цифры в каждом разряде. Если число содержит нечётное количество цифр, в данном случае "7" состоит из одной цифры. В этом случае нужно приписать слева от цифры ноль. Теперь нужно извлечь квадратный корень с недостатком из левого разряда по 2 цифры - это значит, что нужно извлечь квадратный корень из наибольшего целого числа, не превосходящего "7", из которого корень извлекается, извлекается корень из 4, √4 = 2, записываем "2" после знака "равно", а "4" приписываем под первым разрядом и вычитаем (7 - 4 = 3).Далее ставим разделительную черту, и справа от "3" записываем ещё две цифры следующего разряда, но у нас больше нет цифр, значит, дописываем мысленно после "7" запятую, а после запятой два нуля, и эти два нуля сносим к нашей цифре "3" ⇒ 300. Так как мы снесли эти два нуля после запятой, то нужно после "2" не забыть поставить запятую и продолжить извлечение корня.Для того чтобы продолжить вычисления, необходимо умножить "2" на 2 ⇒ "4" и записать слева от черты. После полученной "4" ставим звёздочку, под звёздочкой ещё одну звёздочку.Теперь надо подобрать, какую цифру нужно поставить вместо этой звёздочки так, чтобы произведение этого двузначного числа (4*) на однозначное (*) не превосходило бы "300", но было бы при этом максимальным. Возьмём 7, 47•7 = 329 > 300 - не подходит, берём 6, 46•6 = 276 < 300 - подходит (максимальное) и теперь вычитаем (300 - 276 = 24). То, что вместо звёздочки записали, это как раз будет следующая цифра в нашем корне.Дальше то же самое, сносим следующие две цифры следующего разряда, то есть ещё два нуля, получаем "2400". Умножаем число "26" на 2, не обращая внимание на запятую ⇒ "52", оставляем место для звёздочки. Вместо звёздочки подбираем такую цифру, чтобы " 52*•* " не превысило бы "2400", берём 4, 524•4 = 2096 - подходит (максимальное) и вычитаем (2400 - 2096 = 304). То, что вместо звёздочки записали, записываем в результат. Дальше то же самое, см. приложение. В итоге получаем приближённое значение, √7 ≈ 2,6457513 ≈ 2,64 ≈ 2,6, а насколько находить приближённое значение квадратного корня, это уже на ваше предпочтение.Вначале метод кажется очень сложным, но в ходе систематического её применения, можно легко извлекать квадратные корни столбиком. Метод работает и для чисел, из которых квадратный корень извлекается нацело и необходимо найти это извлечение (см. приложение). После прочтения "плана" можно задасться вопросом, почему ж мы в процессе извлечения корня умножали на 2 ? Если мы извлекали бы корень третьей степени, то умножали бы на 3, если пятой степени, на 5 и т.д. И вместо звёздочек можно ставить точки. Конечно, есть ещё один метод извлечения квадратных корней, легче, при формулы квадрата суммы, но этот метод стоит времени.

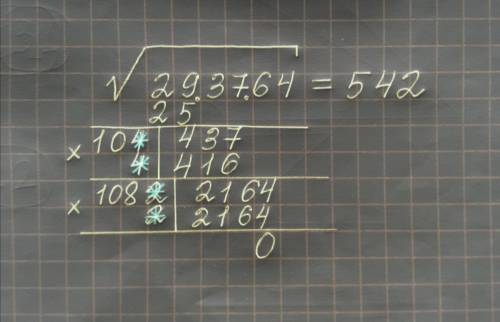
abcd=ab+bc+cd=+a+b+c