![\beta\in[0;1]:\\ \alpha\geq 0: \lim\limits_{n\to\infty}\sqrt[n]{\dfrac{\alpha^n}{\beta^n+n}}=\lim\limits_{n\to\infty}\sqrt[n]{\dfrac{\alpha^n}{n}}=\alpha](/tpl/images/1121/0389/0e53a.png)
Тогда, по признаку Коши, при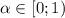 
ряд сходится, при 
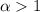расходится.
При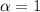 
имеем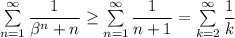 
Гармонический ряд расходится, а тогда исходный ряд расходится по признаку сравнения.
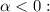
При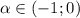 
ряд сходится, т.к. ряд из модулей (по доказанному выше) сходится.
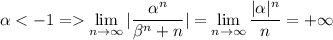необходимое условие не выполнено, а значит ряд расходится.
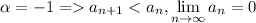, а тогда по признаку Лейбница ряд сходится.
![\beta1:\\ \alpha\geq 0: \lim\limits_{n\to\infty}\sqrt[n]{\dfrac{\alpha^n}{\beta^n+n}}=\lim\limits_{n\to\infty}\sqrt[n]{\dfrac{\alpha^n}{\beta^n}}=\dfrac{\alpha}{\beta}](/tpl/images/1121/0389/8e2ed.png)
Тогда при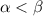 
ряд сходится, при 
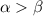расходится.
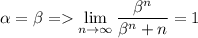- необходимое условие не выполнено, ряд расходится.
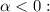
Тогда при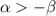 
ряд сходится.
При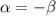 
необходимое условие не выполнено, ряд расходится.
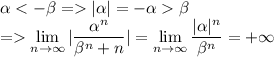необходимое условие не выполнено, ряд расходится.
По итогу ряд сходится только на ![[-1;1)\times[0;1] \;\;\bigcup\;\; (-\beta;\beta)\times[\beta;+\infty),\forall\beta1](/tpl/images/1121/0389/77aa2.png)
Внутренняя граница дорожки - периметр футбольного поля
Внешняя граница дорожки - периметр вокруг поля,окруженного дорожкой
х - ширина футб.поля
3х - длина футб.поля
у - ширина футб.поля, окруженного дорожкой
3у - длина футб.поля,окруженного дорожкой
(3х+х)*2=8х - периметр футбольного поля
(3у+у)*2=8у - периметр футбольного поля,окруженного дорожкой
8у-8х=40
у-х=5
у=х+5
От площади поля с дорожкой вычесть площадь поля-останется площадь дорожки=2100м
3х*х=3х2 - площадь поля
3у*у=3у2
у=х+5
3(х+5)^2=3(х2+10х+25)=3х2+30х+75 - площадь поля с дорожкой
3х2+30х+75 - 3х2 =2100
30х=2025
х=2025:30
х=67,5(м) - ширина поля
67,5*3=202,5 - длина поля
202,5*67,5=13668,75(м2) - площадь футбольного поля
