Рассмотрим первое неравенство:
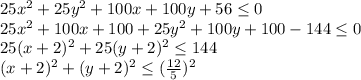
Это круг с центром (-2; -2) и радиусом 2,4.
Рассмотрим второе неравенство:
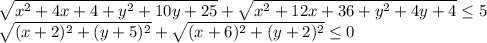
Первый корень — это расстояние от точки (-2; -5) до некоторой точки (x; y). Второй корень — это расстояние от точки (-6; -2) до этой же точки. Значит, левая часть — это сумма расстояний от точек (-2; -5) и (-6; -2) до некоторой точки. Минимальное такое расстояние — это расстояние между самими этими точками (то есть случай, когда точка лежит между известными точками) — равно 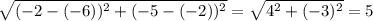 . Но по неравенству сумма расстояний не превосходит 5. Значит, оно равно 5 и задаёт множество точек, лежащих на отрезке, соединяющем точки (-2; -5) и (-6; -2) (то есть задаёт сам этот отрезок).
. Но по неравенству сумма расстояний не превосходит 5. Значит, оно равно 5 и задаёт множество точек, лежащих на отрезке, соединяющем точки (-2; -5) и (-6; -2) (то есть задаёт сам этот отрезок).
Найдём точки пересечения окружности и прямой, содержащей отрезок (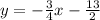 ).
).
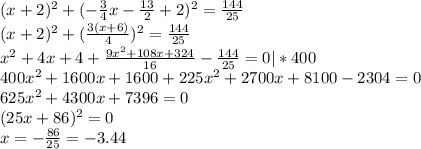
Решение ровно одно, значит, происходит касание. К тому же окружность касается именно отрезка, так как -6 < x < -2
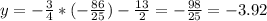
ответ: (-3,44; -3,92)
5%=0,05
20%=0,2
100%=0,1
7,5%=0,075
200%=0,2
72%=0,72
25%=0,25
8%=0,08
50%=0,5
75%=0,75
22,5%=0,225
750%=0,75