Решите в трёх ящиках 64,5 кг яблок.во втором ящике на 2,8 кг больше,чем в первом, а в третьем на 4,6 кг больше, чем во втором.сколько килограмов яблок в каждом ящике?

👇

Ответ:

BunraccoonXD

28.11.2020

Х(кг)- в первом ящике
х+2,8(кг)- во втором ящике
х+2,8+4,6=х+7,4(кг)- в третьем ящике
всего 64,5 кг
х+х+2,8+х+7,4=64,5
3х+10,2=64,5
3х=64,5-10,2
3х=54,3
х=54,3:3
х=18,1(кг)- яблок в первом ящике
18,1+2,8=20,9(кг)- яблок вов тором ящике
20,9+4,6=25,5(кг)- яблок в третьем ящике

18,1+20,9+25,5=64,5(кг)- всего

4,5(99 оценок)

Открыть все ответы

Ответ:

Bioloqq

28.11.2020

Пошаговое объяснение:

1)y= (√x+1 )+ 2/(x-4)

a) первое ограничение на √x - здесь х ≥ 0

б) второе ограничение на знаменатель (х-4) ≠ 0 - здесь х≠ 4

объединяем, получаем ООФ

{x ∈R: x ≥ 0; x≠4}

2)y= (√6-x) + 2/(x²-6x)

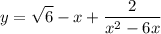
$\displaystyle y = \sqrt{6} -x+\frac{2}{x^2-6x}$

здесь ограничение только на знаменатель (x²-6x) = х(х-6)≠ 0

х ≠ 0 и х ≠ 6

{x ∈R: х ≠ 0; х ≠ 6}

3)y= (√x-2) - x+8/x-5

аналогично первому примеру ограничения на подкоренное выражение х ≥ 0 и на знаменатель (х-5) ≠ 0 ⇒ х ≠ 5

{x ∈R: x ≥ 0; x≠5}

примечание:

если бы скобки были расставлены иначе, например,

не так 1) y= (√x+1 )+ 2/(x-4)

а вот так 1)y= √(x+1 )+ 2/(x-4),

то область определения была бы другая

вот такая {x ∈R: x ≥ -1; x≠4}

4,8(100 оценок)

Ответ:

LoveSmile78900987

28.11.2020

Можно найти несколько пределов данной числовой последовательности. Для этого нужно посмотреть, что произойдет с ней при стремлении к бесконечности с разными знаками, и в "опасных" точках.

"Опасные" точки сразу видны, это:
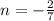1) $n=- \frac{2}{7}$ - знаменатель обращается в 0.
2) n=0

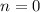- по обычаю проверяется эта точка.

Эта числовая последовательность может быть сведена ко второму замечательному пределу для нахождения пределов:
$lim (1+ \frac{1}{x})^x=e$ (при

→∞)

Выделяем целую часть в дроби:

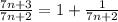
$\frac{7n+3}{7n+2 } = 1 + \frac{1}{7n+2 }$

Используем свойство 2-го замечательного предела, но добавляем степени:

$lim (1 + \frac{1}{7n+2 })^{3n-4}$

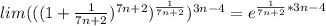$lim (((1 + \frac{1}{7n+2 })^{7n+2})^{ \frac{1}{7n+2}})^{3n-4} = e^{\frac{1}{7n+2} * 3n-4}$ (при

→∞)

То есть мы степень не меняли: домножили и разделили.

Посчитаем, что получилось:

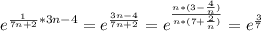$e^{\frac{1}{7n+2} * 3n-4} = e^{ \frac{3n-4}{7n+2}} = e^{ \frac{n*(3-\frac{4}{n}) }{n*(7+\frac{2}{n})} } = e^{ \frac{3}{7} }$ (при

→∞)

Итак:
1)

→+∞ предел равен $e^{ \frac{3}{7} }$
2)

→-∞ предел равен $e^{ \frac{3}{7} }$

3)

→0 предел равен:
$lim ( \frac{7n+3}{7n+2})^{3n-4} = (\frac{3}{2})^{-4} = (\frac{2}{3})^{4} = \frac{16}{81}$

4)

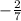
→ $- \frac{2}{7}$
По правило Лопиталя имеем: 0 (не расписывал, поскольку это очень много и неважно в данном случае, нас это не интересует).

Мы видим, что при стремлении к бесконечности с разными знаками, мы имеем конечное число. В "опасных" точках, скачков нет.

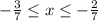Используя свойства показательной функции, находим, что график делает скачок в некотором интервале (основание должно быть неотрицательным числом, если же взять число из интервала $- \frac{3}{7} \leq x \leq - \frac{2}{7}$ - мы получаем отрицательное основание).

Можно говорить, что данная числовая последовательность является неограниченной (из-за этого интервала).

Если же этого не учитывать, то данная числовая последовательность является ограниченной (это очень грубо).

Найдите предел числовой последовательности. укажите, является ли заданная числовая последовательност