Предположим, что так нарисовать можно. Посчитаем общее количество точек пересечения: 3 точки у первой прямой, 3 точки у второй прямой, и так далее, и 3 точки у седьмой прямой. Итого: 3·7=21 точка.
Но каждую точку мы посчитали дважды. Например, точку пересечения первой и второй прямой мы считали и как точку, относящуюся к первой прямой, и как точку, относящуюся ко второй прямой. Значит, реальное их число вдвое меньше. Но 21 - нечетное число. Значит, расчетное реальное число точек пересечения дробное, чего быть не может.
Противоречие. Значит предположение неверное, и такое изображение невозможно.
ответ: нет, нельзя
Рассмотрим число 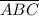 .
.
Поскольку по условию средняя цифра должна быть больше суммы крайних цифр, то выберем в качестве В максимально возможную цифру, то есть 9.
Далее выгодно выбрать в качестве А и С наименьшие числа. В последовательных числах А меняется реже, поэтому сначала выберем А. В качестве А возьмем минимально возможную цифру - цифру 1.
Теперь в качестве С возьмем минимально возможную цифру - цифру 0. Получим число 190, для которого выполняется поставленное условие. Рассматривая следующие числа, получим, что это же условие выполняется для чисел 191, 192, ..., 197, но уже не выполняется для числа 198. Итого: 8 чисел - от 190 до 197 включительно.
Если увеличить А, то даже при минимальном значении С сумма А+С будет больше, чем в уже рассмотренном случае, а значит такой же длинной цепочки чисел получить не удастся.
ответ: 8
У куба 6 равных граней - квадратов. В каждой вершине сходятся 3 грани.
У октаэдра 8 граней: равные равносторонние треугольники. В каждой вершине сходятся 4 грани.
У додекаэдра 12 граней: равные правильные пятиугольники. В каждой вершине сходятся 3 грани.
У икосаэдра 20 граней: равные равносторонние треугольники. В каждой вершине сходятся 5 граней.